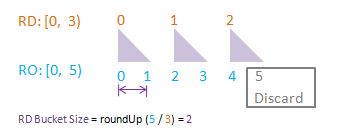
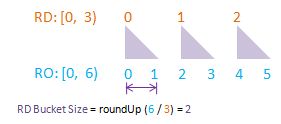
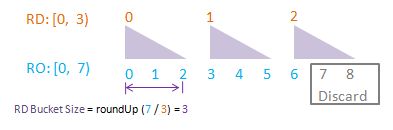
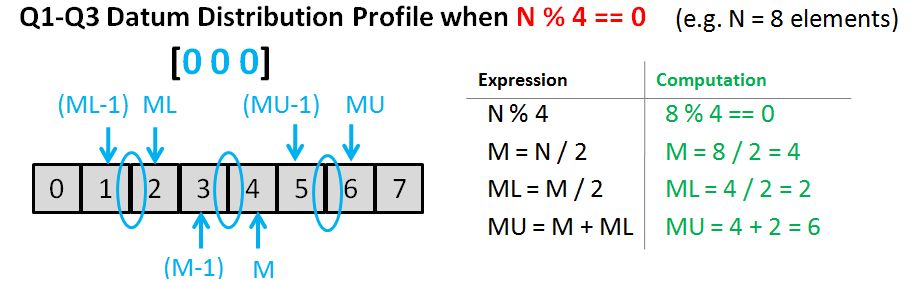
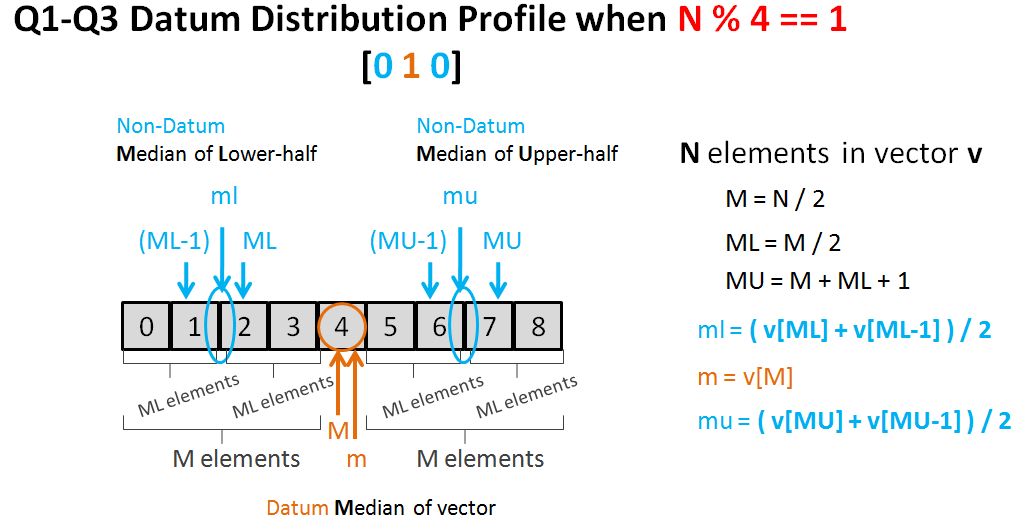
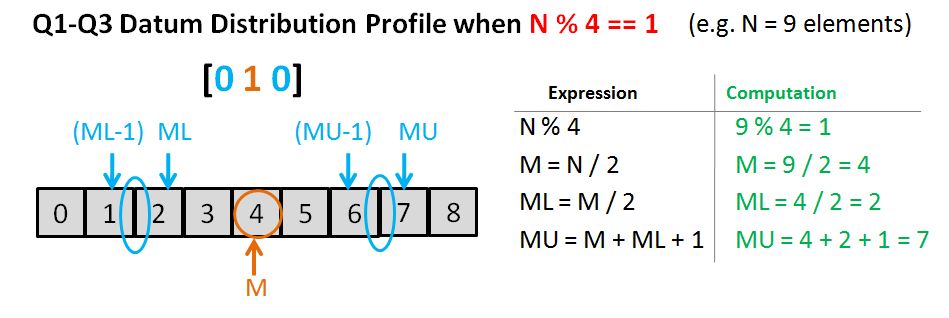
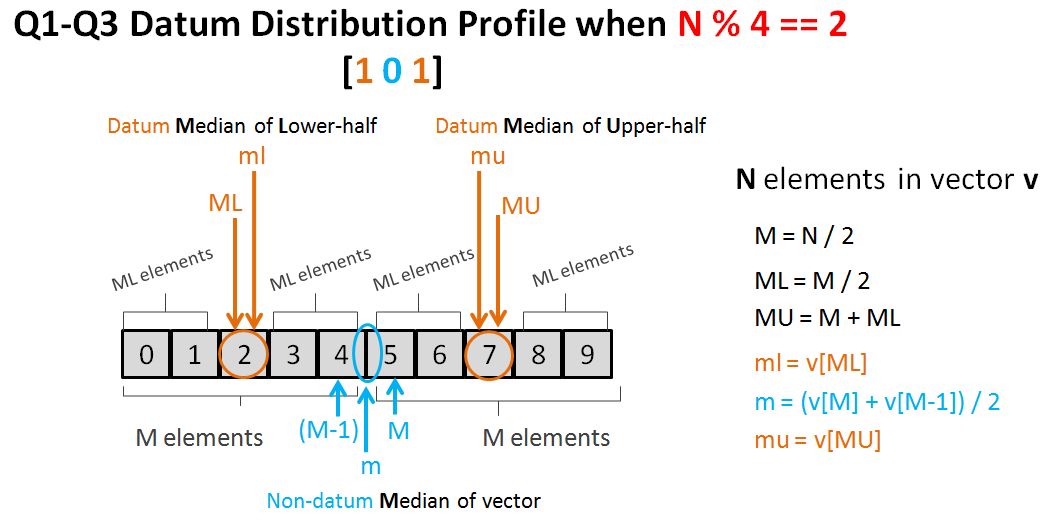
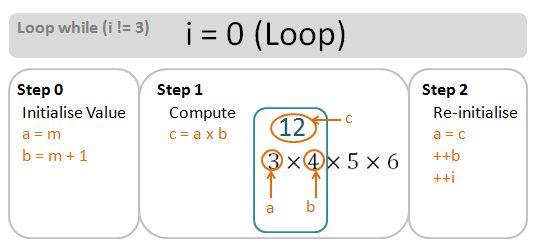
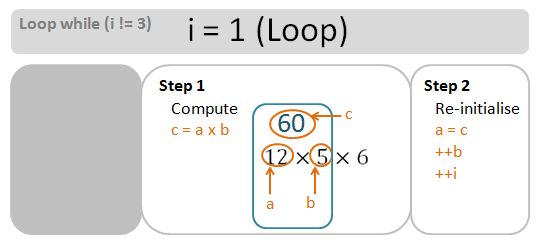
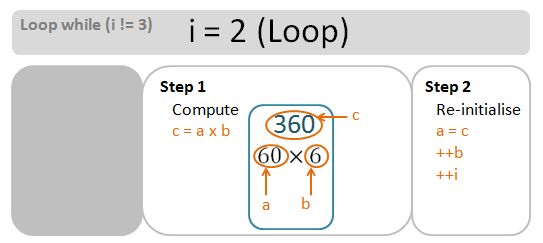
Exercise 5-1
Design and implement a program to produce a permuted index. A permuted index is one in which each phrase is indexed by every word in the phrase. So, given the following input,
The quick brown fox
jumped over the fence
the output would be
The quick brown fox
jumped over the fence
The quick brown fox
jumped over the fence
jumped over the fence
The quick brown fox
jumped over the fence
The quick brown fox
A good algorithm is suggested in The AWK Programming Language by Aho, Kernighan, and Weinberger (Addison-Wesley, 1998). That solution divides the problem into three steps:
Step 1
Read each line of the input and generate a set of rotations of that line. Each rotation puts the next word of the input in the first position and rotates the previous first word to the end of the phrase. So the output of this phrase for the first line of our input would be:
The quick brown fox
quick brown fox The
brown fox The quick
fox The quick brown
Of course, it will be important to know where the original phrase ends and where the rotated beginning begins.
Step 2
Sort the rotations.
Step 3
Un-rotate and write the permuted index, which involves finding the separator, putting the phrase back together, and writing it properly formatted.
Solution
The key to solving this problem is to first know what the problem is. The author is asking us to build a Permuted Index Page that will allow us to easily identify the position of a word within the given text. Think of it of the index page at the back of the book.
What is a Permuted Index Page?
This Wikipedia page has really helped me out a lot in understanding what a Permuted Index Page (a.k.a Key Word In Context Page, or KWIC Page) look like. (Note: the following two snapshots are originated from the Wikipedia page so all rights go to Wikipedia. I have merely annotated the snapshots to aid understanding what a Permuted Index Page look like – which I believe is vital in helping us to solve the problem. So thank you Wikipedia!)
Ok. Assume we have the following “article”:

A Permuted Index Page may look like this:

A Permuted Index Page lists the Permuted Indices (in bold text), sorted in alphabetical order for ease of lookup. Nice thing about a Permuted Index Page is that it allows us not only to find out quickly where the Permuted Index (a.k.a Key Word in Context (KWIC)) “word” is with respect to the article, it also exposes some texts one the left and right of the Permuted Index.
Think of a Google search. When we do a Google Search of a word, Google not only returns us with the potential web addresses, it also “exposes” some texts on the left and right of that search word (which is essentially equivalent to a Permuted Index in our case).
In C++ implementation term, it might be clearer if I draw around that Wikipedia table. This will hopefully give us more clues as to what our C++ implementation might be like.

What may our Permuted Index Page look like?
So coming back to our case. We have the following “article”.
The quick brown fox
jumped over the fence
Our “ultimate” output, a Permuted Index Page, may look like this:
******************* ************************* ********** **********
* The quick * * brown fox * * Line 0 * * Word 2 *
* jumped over the * * fence * * Line 1 * * Word 3 *
* The quick brown * * fox * * Line 0 * * Word 3 *
* * * jumped over the fence * * Line 1 * * Word 0 *
* jumped * * over the fence * * Line 1 * * Word 1 *
* The * * quick brown fox * * Line 0 * * Word 1 *
* jumped over * * the fence * * Line 1 * * Word 2 *
* * * The quick brown fox * * Line 0 * * Word 0 *
******************* ************************* ********** **********
Or in the form of a picture (for clarity sake):

The Permuted Index Page listed above is the output of my C++ program. “Block 1” and “Block 2” essentially are what the Author asks us to produce. “Block 3” and “Block 4” are the “extras” that I decided to incorporate at the time of writing that C++ program – I just wanted to challenge myself and make the output a little bit more “perfect” let say!
To be able to use this output (a Permuted Index Page), we first need to know that the first words of “Block 2” are the Permuted Indices. i.e. the red bold words in the picture!
So, if I want to know where the word “fox” appear in the article, I look up “fox” in the Permuted Index page. It says the word “fox” is on Line 0, word 3. (recall we use a standard index convention in which the first line is called line 0. The second line is called line 1. And so on). The word “fox” is indeed the 3rd word on line 0.
Let’s try another one. Where does the word “over” appear? Easy. Line 1, Word 1 (i.e. second line, second word).
Where does the word “The” appear? Again, easy. Line 0, Word 0. (i.e. First line, first word).
Note that when we do the sort (against the red bold indices), we incorporate into our program to sort regardless of upper or lower case. I will expand a little bit later on how we do this (it’s very easy). All we need to know for now is that it is possible to sort regardless of upper / lower case.
C++ Algorithm and Implementation Strategy
Ok. Now we know what a Permuted Index Page is (and its purpose), what it looks like, and how we use it, let me show you my C++ algorithm and implementation strategy. There are many ways to do this. Some people may prefer maximum efficiency program for best performance. Some may prefer shortest program. When I write my program I aim to make it easiest to understand and easy to follow. I believe the best “beginner” program is the simplest and stupidest program (KISS – “Keep It Simple and Stupid”). That says, there are plenty of opportunities for improvements. But I believe a simple-to-understand program is always a good starting baseline.
The High Level Main Program
Do a quick skimp through of this main program without worrying too much about the details. I have written the main program with the aim that whoever reads the program, he/she should be able to “guess” what each statement tries to achieve without prior knowledge of the details. It aims to summarise the high level logic and I will explain the details a bit more more in the following sections to come.
int main()
{
// read lines via standard console input and append to article
vector<string> article = read_lines();
// prepare an empty Permuted_index_collection
vector<Permuted_index> Permuted_index_collection;
// populate the Permuted_index_collection
make_permuted_index_collection(article, Permuted_index_collection);
// sort the Permuted_index_collection by the rotated_line string (i.e. the permuted index word)
sort_permuted_index_collection(Permuted_index_collection);
// extract and frame the left_block (left align)
vector<string> left_block = frame(get_left_hand_side(Permuted_index_collection),"right",'*');
// extract and frame the right block (right align)
vector<string> right_block = frame(get_right_hand_side(Permuted_index_collection),"left",'*');
// extract and frame the line_number block (left align)
vector<string> line_number_block = frame(get_line_numbers(Permuted_index_collection),"left",'*');
// extract and frame the word_number block (left align)
vector<string> word_number_block = frame(get_word_numbers(Permuted_index_collection),"left",'*');
// horizontal concatenate the blocks to form a permuted index page
vector<string> Permuted_index_collection2 = hcat(left_block, right_block);
vector<string> Permuted_index_collection3 = hcat(Permuted_index_collection2, line_number_block);
vector<string> Permuted_index_collection4 = hcat(Permuted_index_collection3, word_number_block);
// visualise the output
vcout(Permuted_index_collection4);
return 0;
}
Program Logic Step-by-step (in Pictures)
Here, I shall show you the logic that goes behind my own brain when I device this program.
Read the Input Article
I create a simple read function to read the input article (via the Standard Console Input), and parse the article to a vector<string> container – each line within the article is stored as a string object within the vector<string> container.
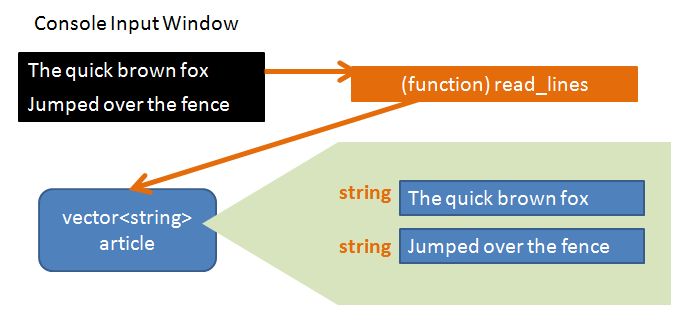
// read lines via standard console input and append to article
vector<string> article = read_lines();
The read function looks like this:
vector<string> read_lines()
{
string line;
vector<string> ret;
while (getline(cin, line))
ret.push_back(line);
return ret;
}
Create Permuted Index Objects
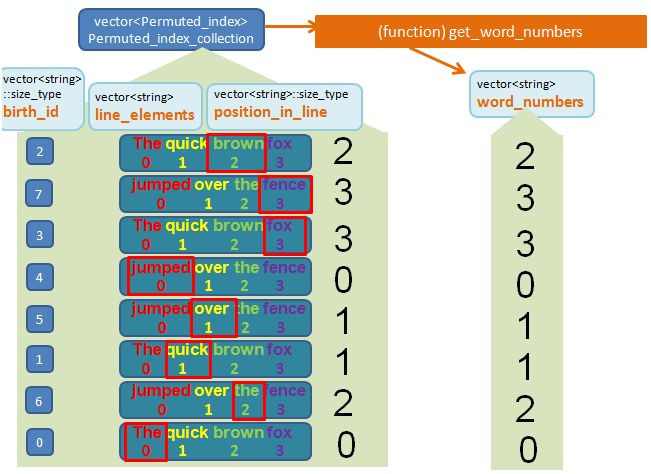
Now that we have the article stored in a vector<string>, our next step is to create a Permuted_index_collection container to store all the required Permuted_index objects (that will be created later on). Each Permuted_index object contains all the required information that we need to represent the particular line in the Permuted Index Page.
Firstly, we need to create an empty vector<Permuted_index> container for storing these Permuted_index objects later on.
// prepare an empty Permuted_index_collection
vector<Permuted_index> Permuted_index_collection;
Now we have our Permuted_index_collection container we need to populate it with Permuted_index objects. We can use the “home-made” function make_permuted_index_collection to create new Permuted_index objects (using the vector<string> article created in the previously as input). This function will populate the vector<Permuted_index> Permuted_index_collection.
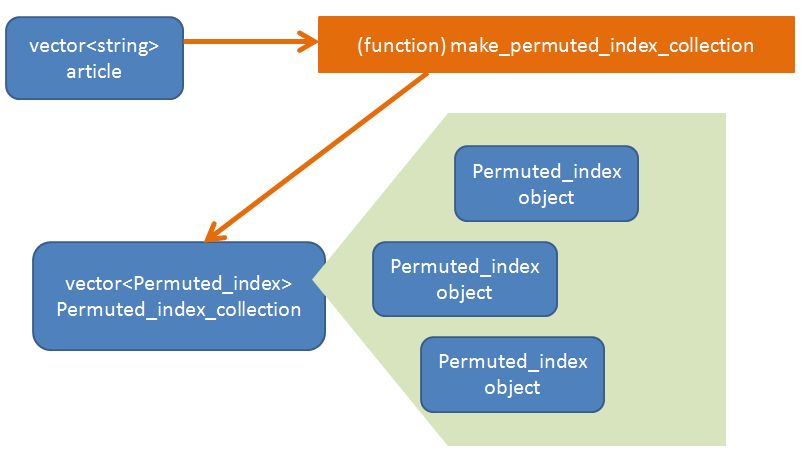
// populate the Permuted_index_collection
make_permuted_index_collection(article, Permuted_index_collection);
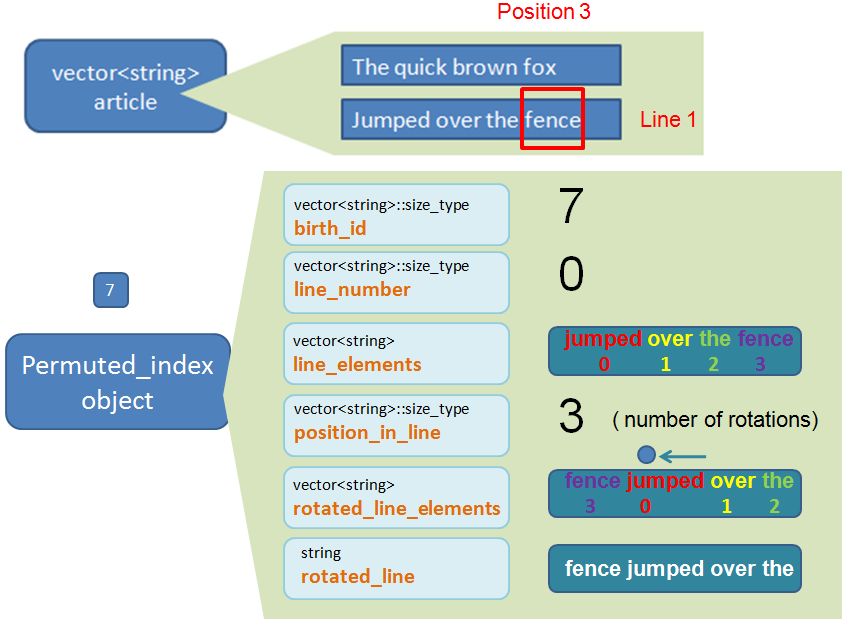
As there are 8 words in the article, it is logical to expect 8 Permuted_index objects in total.
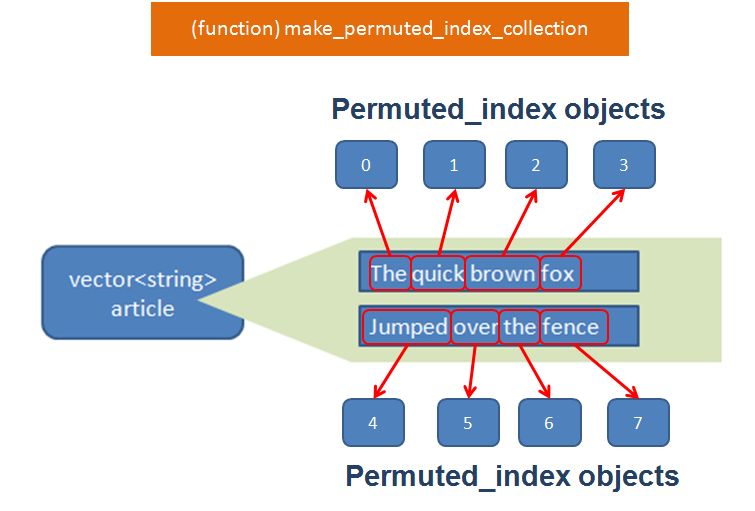
Now, let’s talk more about each individual PermutePermuted_index object. Each Permuted_index object will contain 6 core properties which will be filled in by the function make_permuted_index_collection.
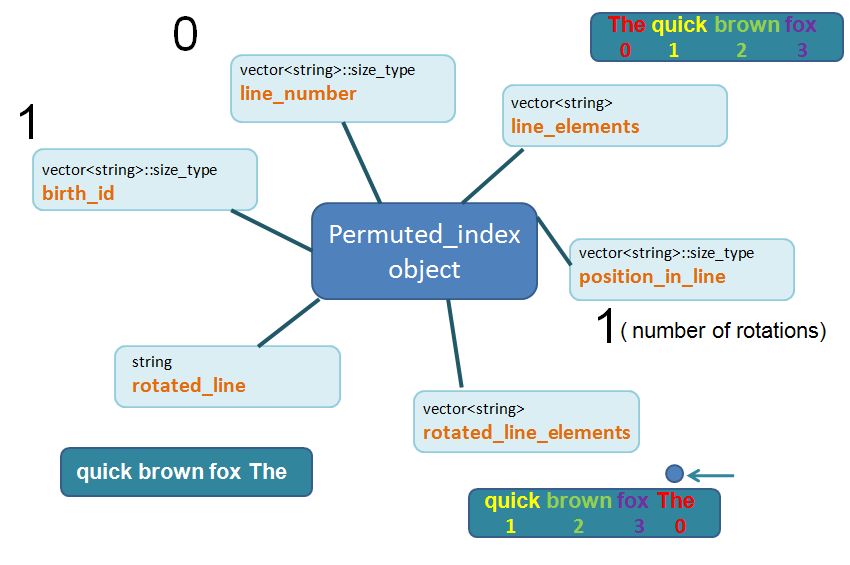
These 6 properties, as we will see later on, will be proven extremely useful for us to construct that Permuted Index Page later on. For now, I will provide a brief description about these 6 properties. (and later on we will see these properties in action!)
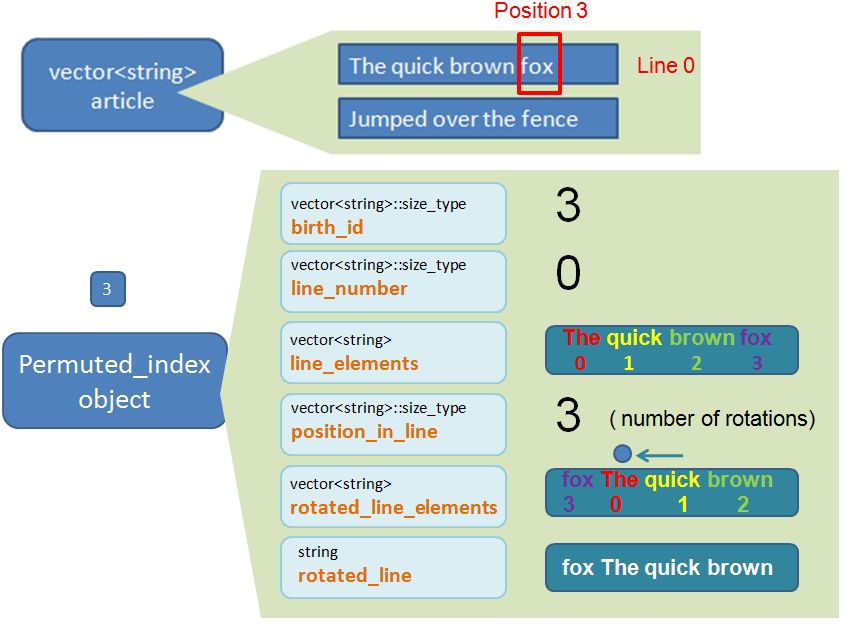
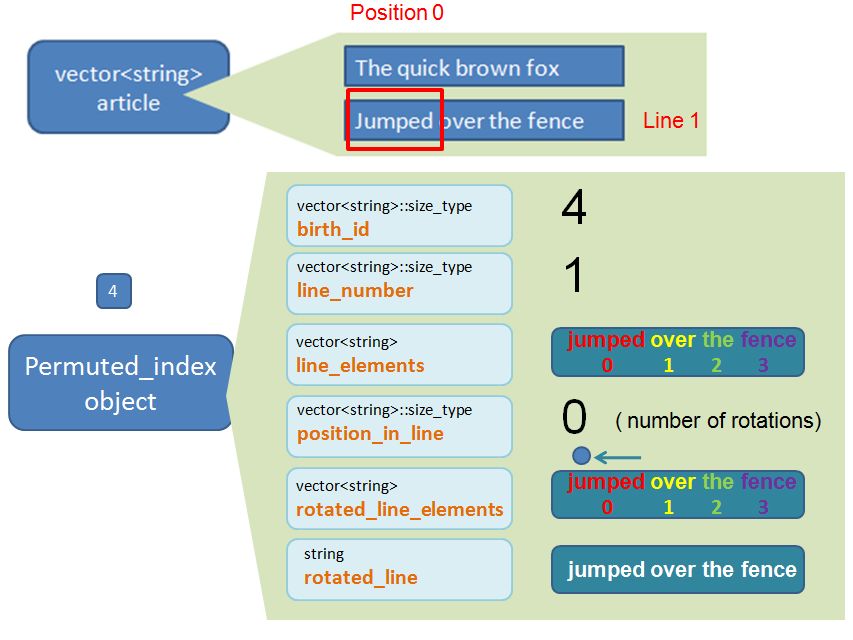
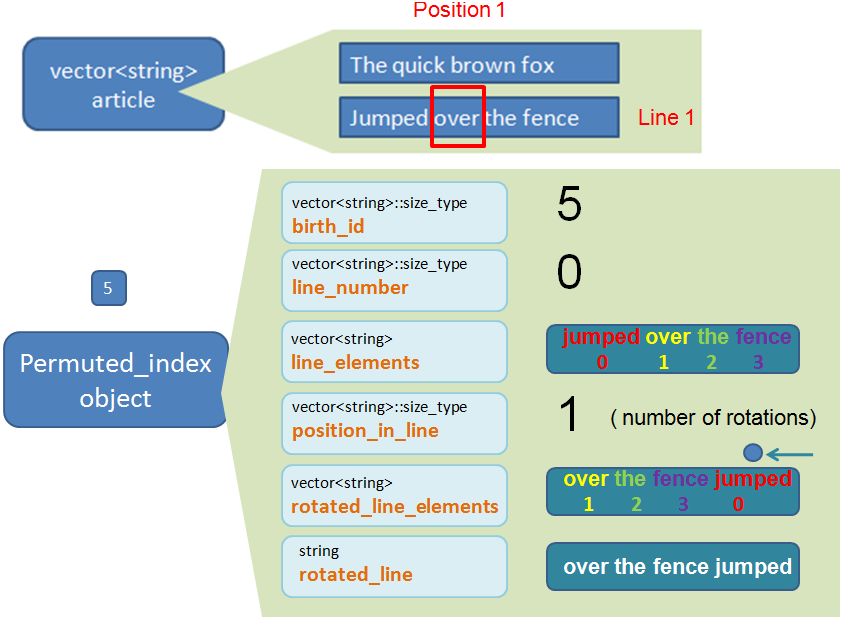
vector<string>::size_type birth_id
The birth_id is number that I assign to the newly created Permuted_index object. This property will not actually be used downstream and is entirely optional. It is purely for me to keep track of the “seniority” of the object. As there are 8 words in the article I would expect to create 8 new Permuted_index objects. The first Permuted_index “born” will be labelled with birth_id 0. The second Permuted_index “born” will be labelled birth_id 1, etc…. the (last) 8th Permuted_index “born” will be labelled birth_id 7.
vector<string>::size_type line_number
There is a clue in the title. It keeps track of which line (within the article) the Permuted_index reside. Remember, line 0 is the first line. Line 1 is the second. Etc.
vector<string> line_elements
This is a vector<string> that contains all the words that appear in that particular line. For example, if this Permuted_index object corresponds to the key word “quick”, the line_elements would be {“The” “quick” “brown” “fox”}. i.e. it is the line that the key word “brown” resides. We store this line as vector<string> instead of string to enable us to generate that Permuted Index Page properly downstream (as you will see later on).
vector<string>::size_type position_in_line
This is the index position where the Permuted Index word appear in the line. Using the same example as above. The permuted index word “quick” corresponds to element 1 (i.e. second element) of the line_element {“The” “quick” “brown” “fox”}. I will demonstrate later on that the position_in_line is effectively the same as the number of rotations that we go through per line.
vector<string> rotated_line_elements
This is what the line_element will look like after we apply the rotations (we mention above that the number of rotations is the same value as position_in_line). Using the same example, if the Permuted_index word is “quick”, which has line_element of {“The” “quick” “brown” “fox”} and position_in_line (i.e. the rotations) of 1. Following a rotation (i.e. shifting words from right to left), the rotated_line_elements will be {“quick” “brown” “fox” “The” }. Notice that the goal of the rotation is to put that permuted index word “quick” to the front (element 0). For now, just accept it when I say, that the sole purpose of the rotated_line_elements is to help us do the “sorting” later on (as explained below).
string rotated_line
This is essentially a string version of the vector<string> rotated_line_elements. It shows what the line looks like after we apply the rotations. Using the same example. If the permuted index word is “quick”, which has rotated_line_element of {“quick” “brown” “fox” “The” }, the rotated_line is effectively “quick brown fox The”. The whole purpose of this property is for us to have a means to sort the Permuted_index objects within the vector<Permuted_index> container, by the rotated_line. i.e. we have a means to have a sorted Permuted Index Page by the Permuted Index words in alphabetical order.
Populate the Permuted Index Collection Container
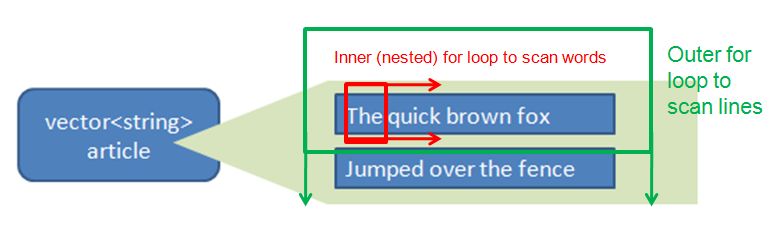
Now, let’s go back to what happen when we use the function make_permuted_index_collection. The function essentially takes the vector<string> article as input, and go through multiple for loops in order to create each Permuted_index object sequentially and fill in the 6 properties (as described above).
There are two for loops.
- The outer for loop iterates through the lines in vector<string> article.
- The inner (nested) for loop iterates through each word along that particular line.
This is what the function make_permuted_index_collection looks like. As you will see, all I am doing here are:
- Create a new Permuted_index object.
- Fill in the 6 properties for the newly created Permuted_index object.
- Add that new Permuted_index object to the vector<Permuted_index> Permuted_index_collection container.
void make_permuted_index_collection(const vector<string>& line_collection,
vector<Permuted_index>& permuted_index_collection)
{
// Input: line_collection
// Output: permuted_index_collection
vector<string>::size_type birth_count = 0;
vector<string>::size_type line_number = 0;
// create Permuted_index object fred one-by-one and parse to the permuted_index_collection
for (vector<string>::size_type i = 0; i != line_collection.size(); ++i)
{
string line = line_collection[i];
vector<string> words = split(line);
// initialise fred's properties before we perform line element rotations
std::vector<std::string>::size_type rotations = 0;
vector<string> ro_words = words;
for (vector<string>::size_type j = 0; j != words.size(); ++j)
{
// Create permuted_index object fred
Permuted_index fred;
fred.birth_id = birth_count;
fred.line_number = line_number;
fred.line_elements = words;
fred.position_in_line = rotations;
fred.rotated_line_elements = ro_words;
fred.rotated_line = string_from_vec_str(ro_words);
// append to the permuted_index_collection
permuted_index_collection.push_back(fred);
// re-initialise
ro_words = rotate_line_elements(ro_words);
++rotations;
++birth_count;
}
++line_number;
}
}
The split function was explained in the text book (S5.6/88) and also in my Solution to Exercise 5-0 (Part 2/3), so I would not repeat here.
Note that fred.line_number and line_number are two different things within the code. fred.line_number corresponds to the property of the Permuted_index object. Whereas line_number corresponds to the local variable within the scope of make_permuted_index_collection. In the code we are simply filling the fred.line_number with the local calculated line_number. Other properties of “fred” are filled in pretty much the same way.
We have a rotate_line_elements function here. This is a “home made” function that I create to rotate the the line_elements – i.e. each rotation shifts the word to the left. If we rotate element 0, it gets rotated to the last element. (it just cycle through).
This is what the rotate_line_element function looks like.
vector<string> rotate_line_elements(const vector<string>& words)
{
vector<string> ret;
typedef vector<string>::size_type vc_sz;
vc_sz size = words.size();
for (vc_sz i = 0; i != size; ++i)
{
if (i == size - 1)
ret.push_back(words[0]);
else
ret.push_back(words[i + 1]);
}
return ret;
}
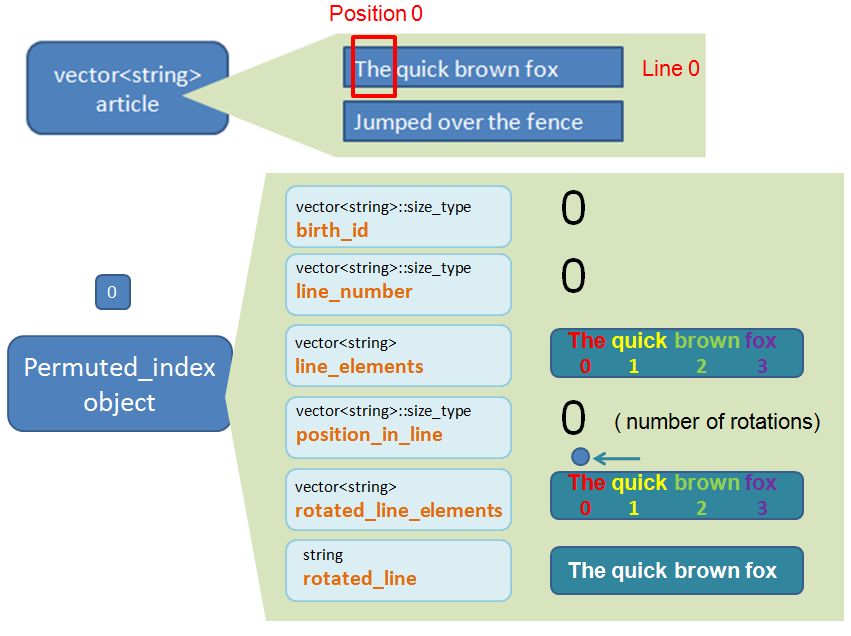
For completeness and understanding sake, the following diagrams summarise the (6 core) properties of the 8 newly created Permuted_index objects, as a result of running the function make_permuted_index_collection.
Permuted_index object 0
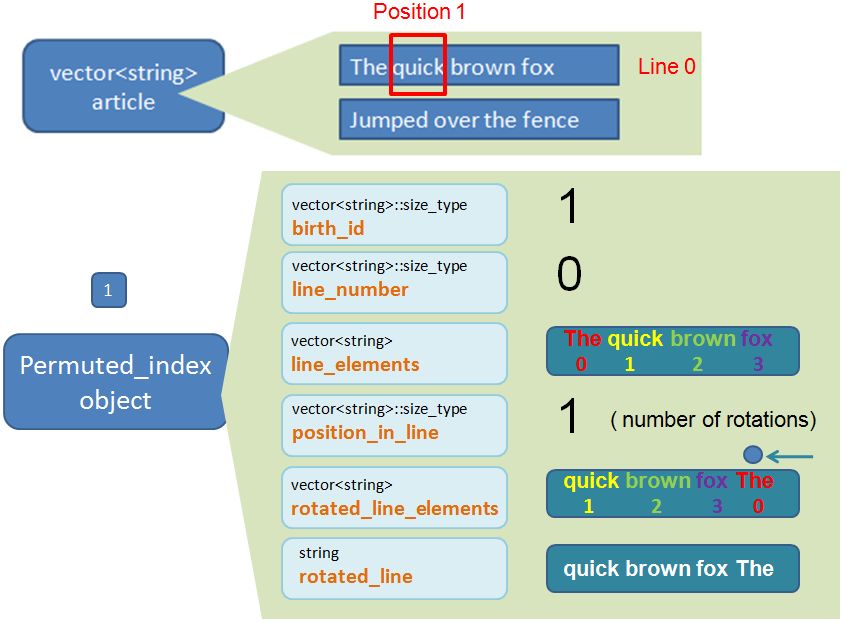
Permuted_index object 1
Permuted_index object 2
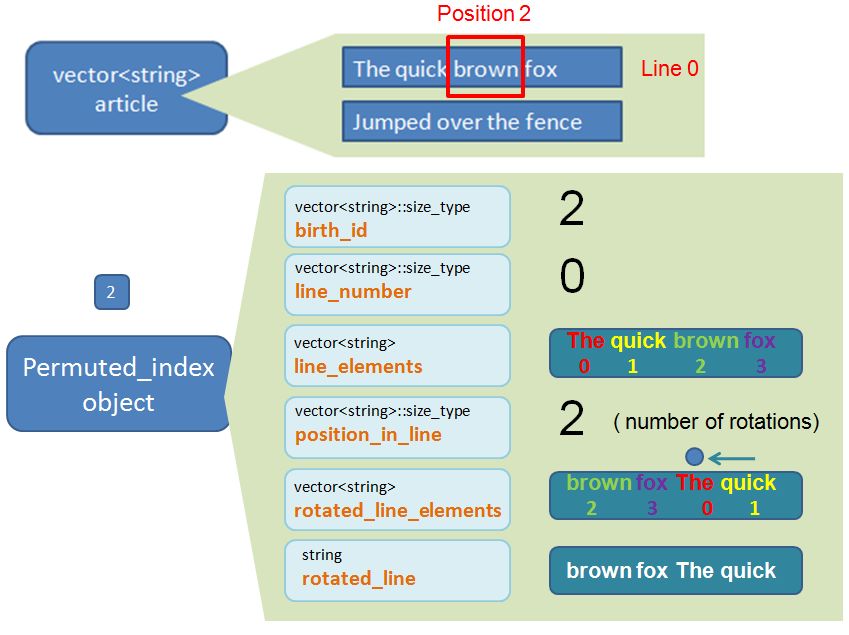
Permuted_index object 3
Permuted_index object 4
Permuted_index object 5
Permuted_index object 6
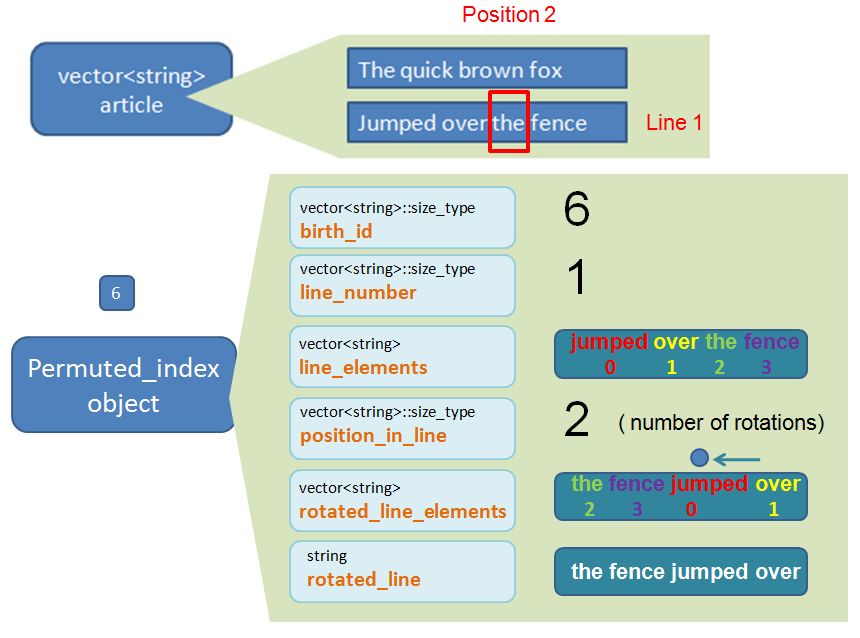
Permuted_index object 7
Sort the Permuted Index Objects
OK. Our vector<string> Permuted_index_collection container is now populated. We are ready to do the sort (so the Permuted_index objects appear in alphabetical order within the Permuted Index Page).
We sort the Permuted_index object by one of its properties, the rotated_line which is of type string.
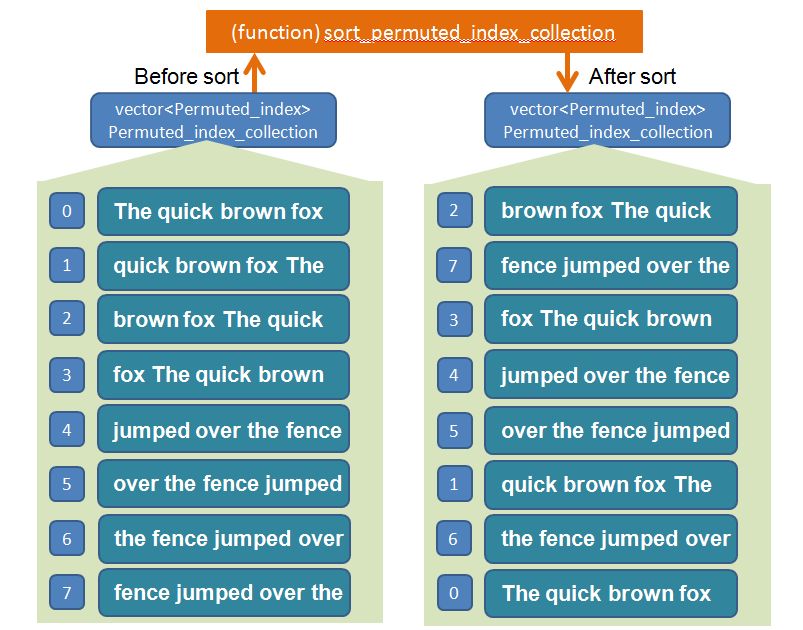
We use a “home made” function sort_permuted_index_collection that helps us do this.
// sort the Permuted_index_collection by the rotated_line string (i.e. the permuted index word)
sort_permuted_index_collection(Permuted_index_collection);
This is what the function sort_permuted_index_collection looks like
void sort_permuted_index_collection(vector<Permuted_index>& x)
{
sort(x.begin(), x.end(), compare);
}
As we are sorting Permuted_index objects by the property rotated_line string, we need to specify the “compare” argument.
bool compare(const Permuted_index& x, const Permuted_index& y)
{
return lowcase(x.rotated_line) < lowcase(y.rotated_line);
}
Because I wish to sort the string regardless of upper or lower case, I use the “home made” lowcase function to essentially convert the strings to lower case before comparing (with the < operator). This way the letter case become insensitive which is what we want.
The “home made” lowcase function looks like this and it essentially converts all the char elements within the string to lower cases (with the help of the standard tolower function)
string lowcase(const string& s)
{
string ret;
for (string::size_type i = 0; i != s.size(); ++i)
{
ret.push_back(tolower(s[i]));
}
return ret;
}
The vector<Permuted_index> container now looks like this:

Each “row” above corresponds to the properties of a Permuted_index object.
Create the “Four Blocks”
Now that our vector<Permuted_index> Permuted_index_collection container is created and sorted, we can use it and create the “four blocks” which we can combine together at the end to form our final Permuted Index Page. Below shows what the “Four blocks” will look like after we have created these.

Note that each block is of type vector<string>. And each string element is of the same width which we can horizontally concatenate them easily later on.
Bearing this diagram in mind, the following sub sections walk through the derivation of the “Four Blocks”, namely
- the Left Hand Block (the “Block 1”)
- the Right Hand Block (the “Block 2”)
- the Line Number Block (the “Block 3”)
- the Word Number Block (the “Block 4”)
To create each block, we do two things:
- Create the vector<string> container and populate with the requirement elements.
- Apply the (enhanced home made) frame function against the vector<string> container to ensure all string elements are of the same (optimum) size (i.e. the width of the “block”). So that when we use the (home made) vcout function to display the vector<string> it appears like a “block” as the empty strings are all padded with empty spaces. The enhanced frame function will have the ability to left-align or right-align the string elements. The frame function will also provide us an option to choose what type of border character that suits our liking. (e.g. it can be a “*”, but it can also be something else if we wish).
The Enhanced Frame Function
The enhanced frame function is built on the original one as per text book (S5.8/93) and also my Solution to Exercise 5-0 (Part 3/3). The enhanced version offer two new options. i.e. (1) Right / Left align string elements, (2) flexible choice of border character. The enhanced frame function looks like this.
vector<string> frame(const vector<string>& v, const string& align, char c)
{
vector<string> ret;
string::size_type maxlen = width(v);
string symbol(1, c);
string border(maxlen + 4, c);
// write the top border
ret.push_back(border);
// write each interior row, bordered by an asterisk and a space
for (vector<string>::size_type i = 0; i != v.size(); ++i)
if (align == "left")
ret.push_back(symbol + " " + v[i] + string(maxlen - v[i].size(), ' ') + " " + symbol);
else if (align == "right")
ret.push_back(symbol + " " + string(maxlen - v[i].size(), ' ') + v[i] + " " + symbol);
// write the bottom border
ret.push_back(border);
return ret;
}
The frame function uses the (home made) width function which is already explained in the text book (S5.8.1/92) and also my Solution to Exercise 5-0 (Part 3/3).
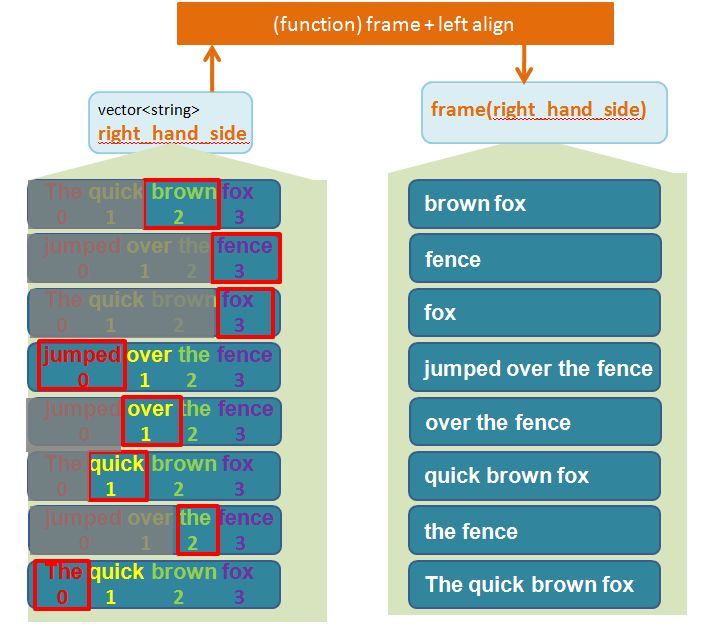
Create the Left Hand Block (the “Block 1”)
// extract and frame the left_block (left align)
vector<string> left_block = frame(get_left_hand_side(Permuted_index_collection),"right",'*');
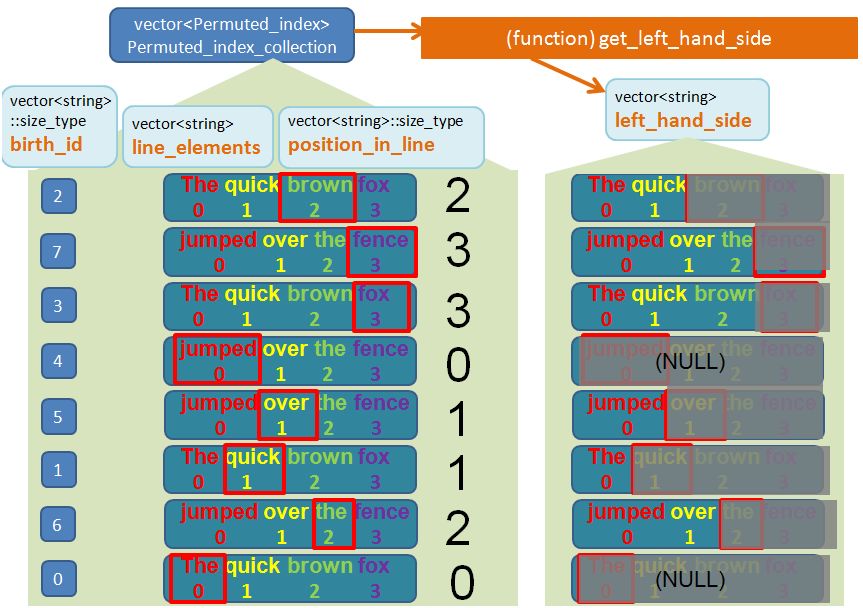
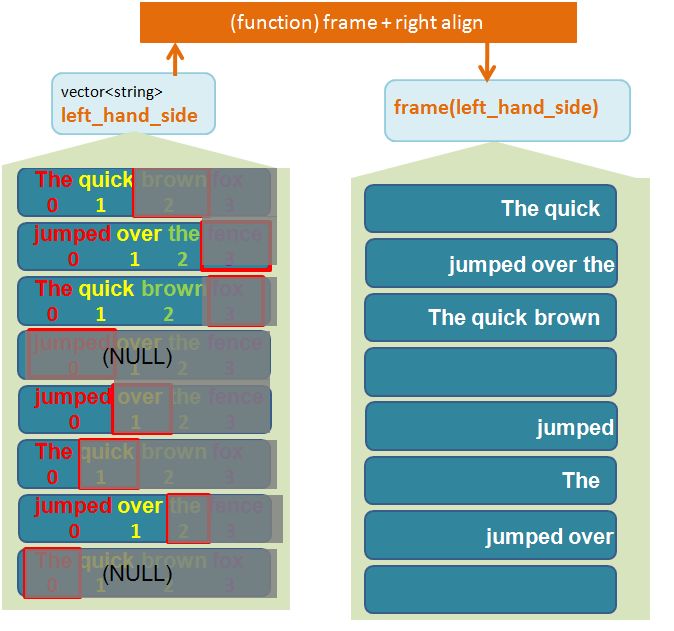
This is what the function get_left_hand_side looks like:
vector<string> get_left_hand_side(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
vector<string> words = iter1->line_elements;
vector<string>::size_type permuted_index_pos = iter1->position_in_line;
string s;
for (vector<string>::size_type i = 0; i != permuted_index_pos; ++i)
{
if (i == 0)
s += words[i];
else
s += (" " + words[i]);
}
ret.push_back(s);
}
return ret;
}
Create the Right Hand Block (the “Block 2”)
// extract and frame the right block (right align)
vector<string> right_block = frame(get_right_hand_side(Permuted_index_collection),"left",'*');
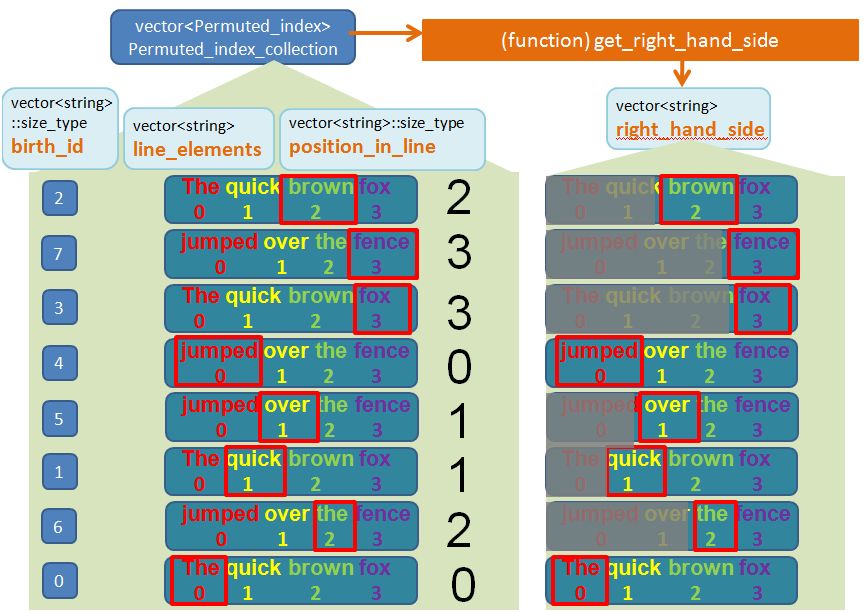
This is what the function get_right_hand_side looks like:
vector<string> get_right_hand_side(const vector<Permuted_index>& v)
{
vector<string> ret;</p>
<pre><code>for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
vector<string> words = iter1->line_elements;
vector<string>::size_type permuted_index_pos = iter1->position_in_line;
string s;
for (vector<string>::size_type i = permuted_index_pos; i != words.size(); ++i)
{
if (i == permuted_index_pos)
s += words[i];
else
s += (" " + words[i]);
}
ret.push_back(s);
}
return ret;
Create the Line Number Block (the “Block 3”)
// extract and frame the line_number block (left align)
vector<string> line_number_block = frame(get_line_numbers(Permuted_index_collection),"left",'*');
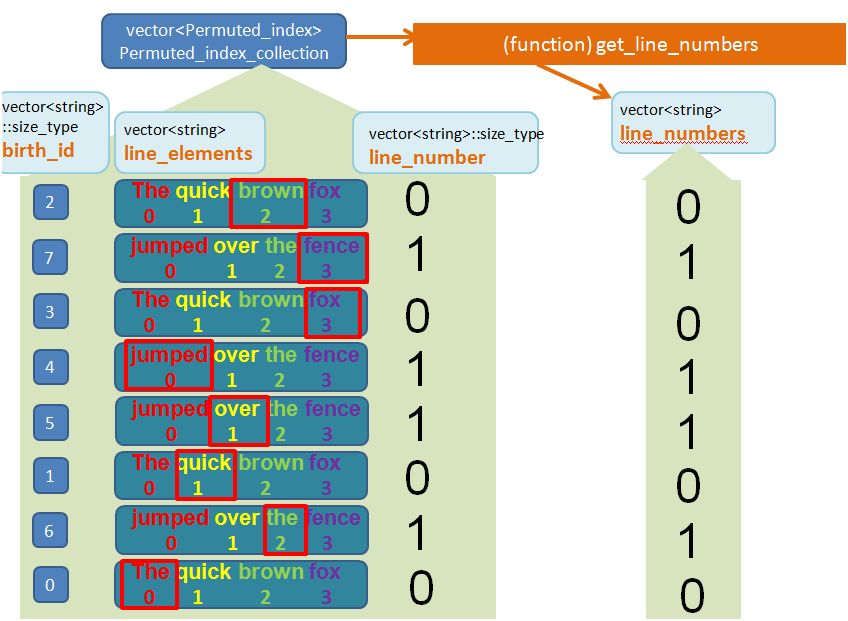
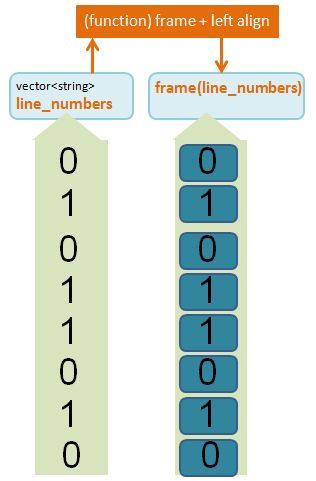
This is what the function get_line_numbers looks like:
vector<string> get_line_numbers(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
string s = "Line " + string_from_vec_str_size_type((iter1->line_number));
ret.push_back(s);
}
return ret;
}
Note that Permuted_index::line_number is of type vector<string>::size_type. I would therefore need to do a conversion to string type. I created this home-made function string_from_vec_str_size_type which will help me to achieve this. The creation of this conversion function is inspired by this page on cplusplus.com.
The function string_from_vec_str_size_type looks like this (it requires the header <sstream> and the std::ostringstream as per the cplusplus.com page)
string string_from_vec_str_size_type(const vector<string>::size_type& any_size_type)
{
string ret; // string which will contain the result
ostringstream convert; // stream used for the conversion
convert << any_size_type; // insert the textual representation of 'Number' in the characters in the stream
ret = convert.str(); // set 'any_integer' to the contents of the stream
return ret;
}
Create the Word Number Block (the “Block 4”)
// extract and frame the word_number block (left align)
vector<string> word_number_block = frame(get_word_numbers(Permuted_index_collection),"left",'*');
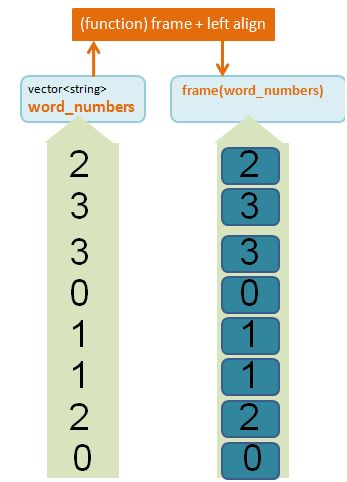
This is what the function get_word_numbers looks like:
vector<string> get_word_numbers(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
string s = "Word " + string_from_vec_str_size_type((iter1->position_in_line));
ret.push_back(s);
}
return ret;
}
Note that Permuted_index::position_in_line is of type std::vector<std::string>::size_type, so we use the home-made function string_from_vec_str_size_type as explained in the previous section above.
Horizontal Concatenate the “Four Blocks”
Recall from the Solution to Exercise 5-0 (Part 3/3), or text book Chapter 5, we have the function hcat already on standby to easily concatenate two vectors horizontally. This is the time to use this hcat function!
Our goal is to horizontally concatenate the “Four Blocks” that we have just created.
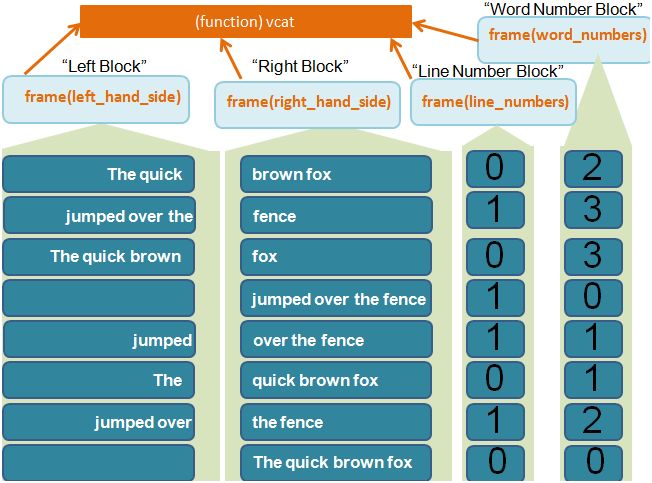
Though we can concatenate the “Four Blocks” all in one pass, for clarity sake I have decided to concatenate two vectors at a time. i.e.
// horizontal concatenate the blocks to form a permuted index page
vector<string> Permuted_index_collection2 = hcat(left_block, right_block);
vector<string> Permuted_index_collection3 = hcat(Permuted_index_collection2, line_number_block);
vector<string> Permuted_index_collection4 = hcat(Permuted_index_collection3, word_number_block);
Display the Permuted Index Page
Now that we have concatenated horizontally the “Four Blocks” into one vector<string> Permuted_index_collection4, let’s display it!
// visualise the output
vcout(Permuted_index_collection4);
I have created a simple function called vcout to help us do this. In fact I created this during my Solution to Exercise 5-0 (Part 3/3) so I am not going to re-explain here.
All we need to know is that, by applying the vcout function against the vector<string> Permuted_index_collection4, we get something like the following in the console output window – a Permuted Index Page!

And this is it!
The Complete Project
To wrap up, let me document this entire Project here, including all the C++ source codes and header files here all in one place.
Source File List
Header File List
Source Files
main.cpp
#include <string> // std::string
#include <vector> // std::vector
#include "read_lines.h" // read_lines
#include "Permuted_index.h" // Permuted_index
#include "split.h" // split
#include "frame.h" // frame
#include "hcat.h" // hcat
#include "vcout.h" // vcout
using std::string;
using std::vector;
int main()
{
// read lines via standard console input and append to article
vector<string> article = read_lines();
// prepare an empty Permuted_index_collection
vector<Permuted_index> Permuted_index_collection;
// populate the Permuted_index_collection
make_permuted_index_collection(article, Permuted_index_collection);
// sort the Permuted_index_collection by the rotated_line string (i.e. the permuted index word)
sort_permuted_index_collection(Permuted_index_collection);
// extract and frame the left_block (left align)
vector<string> left_block = frame(get_left_hand_side(Permuted_index_collection),"right",'*');
// extract and frame the right block (right align)
vector<string> right_block = frame(get_right_hand_side(Permuted_index_collection),"left",'*');
// extract and frame the line_number block (left align)
vector<string> line_number_block = frame(get_line_numbers(Permuted_index_collection),"left",'*');
// extract and frame the word_number block (left align)
vector<string> word_number_block = frame(get_word_numbers(Permuted_index_collection),"left",'*');
// horizontal concatenate the blocks to form a permuted index page
vector<string> Permuted_index_collection2 = hcat(left_block, right_block);
vector<string> Permuted_index_collection3 = hcat(Permuted_index_collection2, line_number_block);
vector<string> Permuted_index_collection4 = hcat(Permuted_index_collection3, word_number_block);
// visualise the output
vcout(Permuted_index_collection4);
return 0;
}
frame.cpp
#include <string> // std::string
#include <vector> // std::vector
#include <algorithm> // std::max
using std::string;
using std::vector;
using std::max;
string::size_type width(const vector<string>& v)
{
string::size_type maxlen = 0;
for(vector<string>::size_type i = 0; i != v.size(); ++i)
maxlen = max(maxlen, v[i].size());
return maxlen;
}
vector<string> frame(const vector<string>& v, const string& align, char c)
{
vector<string> ret;
string::size_type maxlen = width(v);
string symbol(1, c);
string border(maxlen + 4, c);
// write the top border
ret.push_back(border);
// write each interior row, bordered by an asterisk and a space
for (vector<string>::size_type i = 0; i != v.size(); ++i)
if (align == "left")
ret.push_back(symbol + " " + v[i] + string(maxlen - v[i].size(), ' ') + " " + symbol);
else if (align == "right")
ret.push_back(symbol + " " + string(maxlen - v[i].size(), ' ') + v[i] + " " + symbol);
// write the bottom border
ret.push_back(border);
return ret;
}
hcat.cpp
#include <string> // std::string
#include <vector> // std::vector
#include "frame.h" // width
using std::string;
using std::vector;
vector<string> hcat(const vector<string>& left, const vector<string>& right)
{
vector<string> ret;
// add 1 to leave a space between pictures
string::size_type width1 = width(left) + 1;
// indices to look at elements from left and right respectively
vector<string>::size_type i = 0, j = 0;
// continue until we've seen all rows from both pictures
while (i != left.size() || j != right.size())
{
// construct new string to hold characters from both pictures
string s;
// copy a row from the left-hand side, if there is one
if (i != left.size())
s = left[i++];
// pad to full width
s += string(width1 - s.size(), ' ');
// copy a row from teh right-hand side, if there is one
if (j != right.size())
s += right[j++];
// add s to the picture we are creating
ret.push_back(s);
}
return ret;
}
Permuted_index.cpp
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cctype>
#include <sstream> // ostringstream
#include "split.h"
#include "Permuted_index.h"
using std::string;
using std::vector;
using std::cin;
using std::cout;
using std::endl;
using std::tolower;
using std::sort;
using std::ostringstream;
vector<string> rotate_line_elements(const vector<string>& words)
{
vector<string> ret;
typedef vector<string>::size_type vc_sz;
vc_sz size = words.size();
for (vc_sz i = 0; i != size; ++i)
{
if (i == size - 1)
ret.push_back(words[0]);
else
ret.push_back(words[i + 1]);
}
return ret;
}
string string_from_vec_str(const vector<string>& words)
{
string ret;
typedef vector<string>::const_iterator vc_citer;
for (vc_citer iter = words.begin(); iter != words.end(); ++iter)
if (iter == words.begin())
ret += *iter;
else
ret += (" " + *iter);
return ret;
}
void make_permuted_index_collection(const vector<string>& line_collection,
vector<Permuted_index>& permuted_index_collection)
{
// Input: line_collection
// Output: permuted_index_collection
vector<string>::size_type birth_count = 0;
vector<string>::size_type line_number = 0;
// create Permuted_index object fred one-by-one and parse to the permuted_index_collection
for (vector<string>::size_type i = 0; i != line_collection.size(); ++i)
{
string line = line_collection[i];
vector<string> words = split(line);
// initialise fred's properties before we perform line element rotations
std::vector<std::string>::size_type rotations = 0;
vector<string> ro_words = words;
for (vector<string>::size_type j = 0; j != words.size(); ++j)
{
// Create permuted_index object fred
Permuted_index fred;
fred.birth_id = birth_count;
fred.line_number = line_number;
fred.line_elements = words;
fred.position_in_line = rotations;
fred.rotated_line_elements = ro_words;
fred.rotated_line = string_from_vec_str(ro_words);
// append to the permuted_index_collection
permuted_index_collection.push_back(fred);
// re-initialise
ro_words = rotate_line_elements(ro_words);
++rotations;
++birth_count;
}
++line_number;
}
}
string lowcase(const string& s)
{
string ret;
for (string::size_type i = 0; i != s.size(); ++i)
{
ret.push_back(tolower(s[i]));
}
return ret;
}
bool compare(const Permuted_index& x, const Permuted_index& y)
{
return lowcase(x.rotated_line) < lowcase(y.rotated_line);
}
void sort_permuted_index_collection(vector<Permuted_index>& x)
{
sort(x.begin(), x.end(), compare);
}
// (for quick test purpose) use this function to visualise the vector<Permuted_index> collection quickly
void print_permuted_index_collection(const vector<Permuted_index>& collection)
{
for (vector<Permuted_index>::const_iterator iter = collection.begin(); iter != collection.end(); ++iter)
cout << " Permuted_index: " << iter->birth_id
<< " | " << iter->line_number
<< " | " << string_from_vec_str(iter->line_elements)
<< " | " << iter->position_in_line
<< " | " << string_from_vec_str(iter->rotated_line_elements)
<< " | " << iter->rotated_line
<< " | " << iter->line_elements[iter->position_in_line]
<< endl;
}
vector<string> get_left_hand_side(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
vector<string> words = iter1->line_elements;
vector<string>::size_type permuted_index_pos = iter1->position_in_line;
string s;
for (vector<string>::size_type i = 0; i != permuted_index_pos; ++i)
{
if (i == 0)
s += words[i];
else
s += (" " + words[i]);
}
ret.push_back(s);
}
return ret;
}
vector<string> get_right_hand_side(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
vector<string> words = iter1->line_elements;
vector<string>::size_type permuted_index_pos = iter1->position_in_line;
string s;
for (vector<string>::size_type i = permuted_index_pos; i != words.size(); ++i)
{
if (i == permuted_index_pos)
s += words[i];
else
s += (" " + words[i]);
}
ret.push_back(s);
}
return ret;
}
// convert from number to string (http://www.cplusplus.com/articles/D9j2Nwbp/)
string string_from_int(int any_integer)
{
string ret; // string which will contain the result
ostringstream convert; // stream used for the conversion
convert << any_integer; // insert the textual representation of 'Number' in the characters in the stream
ret = convert.str(); // set 'any_integer' to the contents of the stream
return ret;
}
// clone from the same technique. i.e. convert from number to string (http://www.cplusplus.com/articles/D9j2Nwbp/)
// except i have replaced the parameter type from int, to const vector<string>::size_type&
string string_from_vec_str_size_type(const vector<string>::size_type& any_size_type)
{
string ret; // string which will contain the result
ostringstream convert; // stream used for the conversion
convert << any_size_type; // insert the textual representation of 'Number' in the characters in the stream
ret = convert.str(); // set 'any_integer' to the contents of the stream
return ret;
}
vector<string> get_line_numbers(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
string s = "Line " + string_from_vec_str_size_type((iter1->line_number));
ret.push_back(s);
}
return ret;
}
vector<string> get_word_numbers(const vector<Permuted_index>& v)
{
vector<string> ret;
for (vector<Permuted_index>::const_iterator iter1 = v.begin();
iter1 != v.end(); ++iter1)
{
string s = "Word " + string_from_vec_str_size_type((iter1->position_in_line));
ret.push_back(s);
}
return ret;
}
read_lines.cpp
#include <string> // std::string
#include <vector> // std::vector
#include <iostream> // std::cin, std::getline
using std::string;
using std::vector;
using std::cin;
using std::getline;
// Read lines and return the line collection
vector<string> read_lines()
{
string line;
vector<string> ret;
while (getline(cin, line))
ret.push_back(line);
return ret;
}
split.cpp
#include <string> // std::string
#include <vector> // std::vector
#include <cctype> // std::isspace
using std::vector;
using std::string;
using std::isspace;
// scan a string of texts, split into words, return a vector that contains these words.
// (S5.6/88)
vector<string> split(const string& s)
{
vector<string> ret;
typedef string::size_type string_size;
string_size i = 0;
// invariant: we have processed characters original value of [i, i)
while (i != s.size() )
{
// ignore leading blanks
// invariant: characters in range [original i, current i)
while (i != s.size() && isspace(s[i]))
++i;
// find end of next word
string_size j = i;
// invariant: none of the characters in range [original j, current j) is a space
while (j != s.size() && !isspace(s[j]))
++j;
// if we found some non-whitespace characters
if (i != j)
// copy from s starting at i and taking j - i chars
ret.push_back(s.substr(i, j - i));
i = j;
}
return ret;
}
vcout.cpp
#include <iostream> // std::cout, std::endl
#include <string> // std::string
#include <vector> // std::vector
using std::cout;
using std::endl;
using std::string;
using std::vector;
int vcout(const vector<string>& v)
{
for (vector<string>::const_iterator iter = v.begin();
iter != v.end(); ++iter)
{
cout << (*iter) << endl;
}
return 0;
}
Header Files
frame.h
#ifndef GUARD_FRAME_H
#define GUARD_FRAME_H
#include <string>
#include <vector>
std::string::size_type width(const std::vector<std::string>&);
std::vector<std::string> frame(const std::vector<std::string>&, const std::string&, const char);
#endif // GUARD_FRAME_H
hcat.h
#ifndef GUARD_HCAT_H
#define GUARD_HCAT_H
#include <string>
#include <vector>
std::vector<std::string> hcat(const std::vector<std::string>&, const std::vector<std::string>&);
#endif // GUARD_HCAT_H
Permuted_index.h
#ifndef GUARD_PERMUTED_INDEX_H
#define GUARD_PERMUTED_INDEX_H
#include <string>
#include <vector>
struct Permuted_index
{
std::vector<std::string>::size_type birth_id;
std::vector<std::string>::size_type line_number;
std::vector<std::string> line_elements;
std::vector<std::string>::size_type position_in_line;
std::vector<std::string> rotated_line_elements;
std::string rotated_line;
};
bool compare(const Permuted_index&, const Permuted_index&);
std::string string_from_vec_str(const std::vector<std::string>&);
std::string string_from_vec_str_size_type(const std::vector<std::string>::size_type&);
std::string string_from_int(int);
void make_permuted_index_collection(const std::vector<std::string>&, std::vector<Permuted_index>&);
void sort_permuted_index_collection(std::vector<Permuted_index>&);
void print_permuted_index_collection(const std::vector<Permuted_index>&);
std::vector<std::string> rotate_line_elements(const std::vector<std::string>&);
std::vector<std::string> get_left_hand_side(const std::vector<Permuted_index>&);
std::vector<std::string> get_right_hand_side(const std::vector<Permuted_index>&);
std::vector<std::string> get_line_numbers(const std::vector<Permuted_index>&);
std::vector<std::string> get_word_numbers(const std::vector<Permuted_index>&);
#endif // GUARD_PERMUTED_INDEX_H
read_lines.h
#ifndef GUARD_READ_LINES_H
#define GUARD_READ_LINES_H
#include <string>
#include <vector>
std::vector<std::string> read_lines();
#endif // GUARD_READ_LINES_H
split.h
#ifndef GUARD_SPLIT_H
#define GUARD_SPLIT_H
#include <vector>
#include <string>
std::vector<std::string> split(const std::string&);
#endif // GUARD_SPLIT_H
vcout.h
#ifndef GUARD_VCOUT_H
#define GUARD_VCOUT_H
#include <string>
#include <vector>
int vcout(const std::vector<std::string>&);
#endif // GUARD_VCOUT_H
Test Program
This summarises my program test input and output.
Test 1 – The quick brown fox
The quick brown fox
jumped over the fence
^Z
******************* ************************* ********** **********
* The quick * * brown fox * * Line 0 * * Word 2 *
* jumped over the * * fence * * Line 1 * * Word 3 *
* The quick brown * * fox * * Line 0 * * Word 3 *
* * * jumped over the fence * * Line 1 * * Word 0 *
* jumped * * over the fence * * Line 1 * * Word 1 *
* The * * quick brown fox * * Line 0 * * Word 1 *
* jumped over * * the fence * * Line 1 * * Word 2 *
* * * The quick brown fox * * Line 0 * * Word 0 *
******************* ************************* ********** **********
Process returned 0 (0x0) execution time : 33.226 s
Press any key to continue.
Test 2 – Shakespeare’s To be, or Not to be
Just to make sure the program works regardless of article content. let’s try and create a Permuted Index Page for William Shakespeare’s famous poem “To be, or Not to be”. And the program works! (cool isn’t it!)
When he himself might his quietus make
With a bare bodkin? who would fardels bear,
To grunt and sweat under a weary life,
But that the dread of something after death,
The undiscover'd country from whose bourn
No traveller returns, puzzles the will
And makes us rather bear those ills we have
Than fly to others that we know not of?
Thus conscience does make cowards of us all;
And thus the native hue of resolution
Is sicklied o'er with the pale cast of thought,
And enterprises of great pith and moment
With this regard their currents turn awry,
And lose the name of action. - Soft you now!
The fair Ophelia! Nymph, in thy orisons
Be all my sins remember'd.
^Z
************************************************* ****************************************************** *********** **********
* That flesh is heir to, * * 'tis a consummation * * Line 7 * * Word 5 *
* Whether * * 'tis nobler in the mind to suffer * * Line 1 * * Word 1 *
* And lose the name of action. * * - Soft you now! * * Line 32 * * Word 6 *
* With * * a bare bodkin? who would fardels bear, * * Line 20 * * Word 1 *
* That flesh is heir to, 'tis * * a consummation * * Line 7 * * Word 6 *
* Or to take arms against * * a sea of troubles, * * Line 3 * * Word 5 *
* No more; and by * * a sleep to say we end * * Line 5 * * Word 4 *
* To grunt and sweat under * * a weary life, * * Line 21 * * Word 5 *
* And lose the name of * * action. - Soft you now! * * Line 32 * * Word 5 *
* But that the dread of something * * after death, * * Line 22 * * Word 6 *
* Or to take arms * * against a sea of troubles, * * Line 3 * * Word 4 *
* Be * * all my sins remember'd. * * Line 34 * * Word 1 *
* Thus conscience does make cowards of us * * all; * * Line 27 * * Word 7 *
* The slings * * and arrows of outrageous fortune, * * Line 2 * * Word 2 *
* No more; * * and by a sleep to say we end * * Line 5 * * Word 2 *
* * * And by opposing end them? To die: to sleep; * * Line 4 * * Word 0 *
* * * And enterprises of great pith and moment * * Line 30 * * Word 0 *
* * * And lose the name of action. - Soft you now! * * Line 32 * * Word 0 *
* * * And makes us rather bear those ills we have * * Line 25 * * Word 0 *
* And enterprises of great pith * * and moment * * Line 30 * * Word 5 *
* For who would bear the whips * * and scorns of time, * * Line 14 * * Word 6 *
* To grunt * * and sweat under a weary life, * * Line 21 * * Word 2 *
* The insolence of office * * and the spurns * * Line 17 * * Word 4 *
* The heart-ache * * and the thousand natural shocks * * Line 6 * * Word 2 *
* * * And thus the native hue of resolution * * Line 28 * * Word 0 *
* Or to take * * arms against a sea of troubles, * * Line 3 * * Word 3 *
* The slings and * * arrows of outrageous fortune, * * Line 2 * * Word 3 *
* With this regard their currents turn * * awry, * * Line 31 * * Word 6 *
* To sleep: perchance to dream: * * ay, there's the rub; * * Line 9 * * Word 5 *
* With a * * bare bodkin? who would fardels bear, * * Line 20 * * Word 2 *
* * * Be all my sins remember'd. * * Line 34 * * Word 0 *
* Devoutly to * * be wish'd. To die, to sleep; * * Line 8 * * Word 2 *
* To * * be, or not to be: that is the question: * * Line 0 * * Word 1 *
* To be, or not to * * be: that is the question: * * Line 0 * * Word 5 *
* For who would * * bear the whips and scorns of time, * * Line 14 * * Word 3 *
* And makes us rather * * bear those ills we have * * Line 25 * * Word 4 *
* With a bare bodkin? who would fardels * * bear, * * Line 20 * * Word 7 *
* With a bare * * bodkin? who would fardels bear, * * Line 20 * * Word 3 *
* The undiscover'd country from whose * * bourn * * Line 23 * * Word 5 *
* * * But that the dread of something after death, * * Line 22 * * Word 0 *
* No more; and * * by a sleep to say we end * * Line 5 * * Word 3 *
* And * * by opposing end them? To die: to sleep; * * Line 4 * * Word 1 *
* That makes * * calamity of so long life; * * Line 13 * * Word 2 *
* Is sicklied o'er with the pale * * cast of thought, * * Line 29 * * Word 6 *
* When we have shuffled off this mortal * * coil, * * Line 11 * * Word 7 *
* For in that sleep of death what dreams may * * come * * Line 10 * * Word 9 *
* Thus * * conscience does make cowards of us all; * * Line 27 * * Word 1 *
* That flesh is heir to, 'tis a * * consummation * * Line 7 * * Word 7 *
* The oppressor's wrong, the proud man's * * contumely, * * Line 15 * * Word 6 *
* The undiscover'd * * country from whose bourn * * Line 23 * * Word 2 *
* Thus conscience does make * * cowards of us all; * * Line 27 * * Word 4 *
* With this regard their * * currents turn awry, * * Line 31 * * Word 4 *
* For in that sleep of * * death what dreams may come * * Line 10 * * Word 5 *
* But that the dread of something after * * death, * * Line 22 * * Word 7 *
* The pangs of despised love, the law's * * delay, * * Line 16 * * Word 7 *
* The pangs of * * despised love, the law's delay, * * Line 16 * * Word 3 *
* * * Devoutly to be wish'd. To die, to sleep; * * Line 8 * * Word 0 *
* Devoutly to be wish'd. To * * die, to sleep; * * Line 8 * * Word 5 *
* And by opposing end them? To * * die: to sleep; * * Line 4 * * Word 6 *
* Thus conscience * * does make cowards of us all; * * Line 27 * * Word 2 *
* But that the * * dread of something after death, * * Line 22 * * Word 3 *
* To sleep: perchance to * * dream: ay, there's the rub; * * Line 9 * * Word 4 *
* For in that sleep of death what * * dreams may come * * Line 10 * * Word 7 *
* No more; and by a sleep to say we * * end * * Line 5 * * Word 9 *
* And by opposing * * end them? To die: to sleep; * * Line 4 * * Word 3 *
* And * * enterprises of great pith and moment * * Line 30 * * Word 1 *
* The * * fair Ophelia! Nymph, in thy orisons * * Line 33 * * Word 1 *
* With a bare bodkin? who would * * fardels bear, * * Line 20 * * Word 6 *
* That * * flesh is heir to, 'tis a consummation * * Line 7 * * Word 1 *
* Than * * fly to others that we know not of? * * Line 26 * * Word 1 *
* * * For in that sleep of death what dreams may come * * Line 10 * * Word 0 *
* * * For who would bear the whips and scorns of time, * * Line 14 * * Word 0 *
* The slings and arrows of outrageous * * fortune, * * Line 2 * * Word 6 *
* The undiscover'd country * * from whose bourn * * Line 23 * * Word 3 *
* Must * * give us pause: there's the respect * * Line 12 * * Word 1 *
* And enterprises of * * great pith and moment * * Line 30 * * Word 3 *
* To * * grunt and sweat under a weary life, * * Line 21 * * Word 1 *
* And makes us rather bear those ills we * * have * * Line 25 * * Word 8 *
* When we * * have shuffled off this mortal coil, * * Line 11 * * Word 2 *
* When * * he himself might his quietus make * * Line 19 * * Word 1 *
* The * * heart-ache and the thousand natural shocks * * Line 6 * * Word 1 *
* That flesh is * * heir to, 'tis a consummation * * Line 7 * * Word 3 *
* When he * * himself might his quietus make * * Line 19 * * Word 2 *
* When he himself might * * his quietus make * * Line 19 * * Word 4 *
* And thus the native * * hue of resolution * * Line 28 * * Word 4 *
* And makes us rather bear those * * ills we have * * Line 25 * * Word 6 *
* For * * in that sleep of death what dreams may come * * Line 10 * * Word 1 *
* Whether 'tis nobler * * in the mind to suffer * * Line 1 * * Word 3 *
* The fair Ophelia! Nymph, * * in thy orisons * * Line 33 * * Word 4 *
* The * * insolence of office and the spurns * * Line 17 * * Word 1 *
* That flesh * * is heir to, 'tis a consummation * * Line 7 * * Word 2 *
* * * Is sicklied o'er with the pale cast of thought, * * Line 29 * * Word 0 *
* To be, or not to be: that * * is the question: * * Line 0 * * Word 7 *
* Than fly to others that we * * know not of? * * Line 26 * * Word 6 *
* The pangs of despised love, the * * law's delay, * * Line 16 * * Word 6 *
* To grunt and sweat under a weary * * life, * * Line 21 * * Word 7 *
* That makes calamity of so long * * life; * * Line 13 * * Word 6 *
* That makes calamity of so * * long life; * * Line 13 * * Word 5 *
* And * * lose the name of action. - Soft you now! * * Line 32 * * Word 1 *
* The pangs of despised * * love, the law's delay, * * Line 16 * * Word 4 *
* Thus conscience does * * make cowards of us all; * * Line 27 * * Word 3 *
* When he himself might his quietus * * make * * Line 19 * * Word 6 *
* That * * makes calamity of so long life; * * Line 13 * * Word 1 *
* And * * makes us rather bear those ills we have * * Line 25 * * Word 1 *
* The oppressor's wrong, the proud * * man's contumely, * * Line 15 * * Word 5 *
* For in that sleep of death what dreams * * may come * * Line 10 * * Word 8 *
* That patient * * merit of the unworthy takes, * * Line 18 * * Word 2 *
* When he himself * * might his quietus make * * Line 19 * * Word 3 *
* Whether 'tis nobler in the * * mind to suffer * * Line 1 * * Word 5 *
* And enterprises of great pith and * * moment * * Line 30 * * Word 6 *
* No * * more; and by a sleep to say we end * * Line 5 * * Word 1 *
* When we have shuffled off this * * mortal coil, * * Line 11 * * Word 6 *
* * * Must give us pause: there's the respect * * Line 12 * * Word 0 *
* Be all * * my sins remember'd. * * Line 34 * * Word 2 *
* And lose the * * name of action. - Soft you now! * * Line 32 * * Word 3 *
* And thus the * * native hue of resolution * * Line 28 * * Word 3 *
* The heart-ache and the thousand * * natural shocks * * Line 6 * * Word 5 *
* * * No more; and by a sleep to say we end * * Line 5 * * Word 0 *
* * * No traveller returns, puzzles the will * * Line 24 * * Word 0 *
* Whether 'tis * * nobler in the mind to suffer * * Line 1 * * Word 2 *
* Than fly to others that we know * * not of? * * Line 26 * * Word 7 *
* To be, or * * not to be: that is the question: * * Line 0 * * Word 3 *
* And lose the name of action. - Soft you * * now! * * Line 32 * * Word 9 *
* The fair Ophelia! * * Nymph, in thy orisons * * Line 33 * * Word 3 *
* Is sicklied * * o'er with the pale cast of thought, * * Line 29 * * Word 2 *
* And lose the name * * of action. - Soft you now! * * Line 32 * * Word 4 *
* For in that sleep * * of death what dreams may come * * Line 10 * * Word 4 *
* The pangs * * of despised love, the law's delay, * * Line 16 * * Word 2 *
* And enterprises * * of great pith and moment * * Line 30 * * Word 2 *
* The insolence * * of office and the spurns * * Line 17 * * Word 2 *
* The slings and arrows * * of outrageous fortune, * * Line 2 * * Word 4 *
* And thus the native hue * * of resolution * * Line 28 * * Word 5 *
* That makes calamity * * of so long life; * * Line 13 * * Word 3 *
* But that the dread * * of something after death, * * Line 22 * * Word 4 *
* That patient merit * * of the unworthy takes, * * Line 18 * * Word 3 *
* Is sicklied o'er with the pale cast * * of thought, * * Line 29 * * Word 7 *
* For who would bear the whips and scorns * * of time, * * Line 14 * * Word 8 *
* Or to take arms against a sea * * of troubles, * * Line 3 * * Word 7 *
* Thus conscience does make cowards * * of us all; * * Line 27 * * Word 5 *
* Than fly to others that we know not * * of? * * Line 26 * * Word 8 *
* When we have shuffled * * off this mortal coil, * * Line 11 * * Word 4 *
* The insolence of * * office and the spurns * * Line 17 * * Word 3 *
* The fair * * Ophelia! Nymph, in thy orisons * * Line 33 * * Word 2 *
* And by * * opposing end them? To die: to sleep; * * Line 4 * * Word 2 *
* The * * oppressor's wrong, the proud man's contumely, * * Line 15 * * Word 1 *
* To be, * * or not to be: that is the question: * * Line 0 * * Word 2 *
* * * Or to take arms against a sea of troubles, * * Line 3 * * Word 0 *
* The fair Ophelia! Nymph, in thy * * orisons * * Line 33 * * Word 6 *
* Than fly to * * others that we know not of? * * Line 26 * * Word 3 *
* The slings and arrows of * * outrageous fortune, * * Line 2 * * Word 5 *
* Is sicklied o'er with the * * pale cast of thought, * * Line 29 * * Word 5 *
* The * * pangs of despised love, the law's delay, * * Line 16 * * Word 1 *
* That * * patient merit of the unworthy takes, * * Line 18 * * Word 1 *
* Must give us * * pause: there's the respect * * Line 12 * * Word 3 *
* To sleep: * * perchance to dream: ay, there's the rub; * * Line 9 * * Word 2 *
* And enterprises of great * * pith and moment * * Line 30 * * Word 4 *
* The oppressor's wrong, the * * proud man's contumely, * * Line 15 * * Word 4 *
* No traveller returns, * * puzzles the will * * Line 24 * * Word 3 *
* To be, or not to be: that is the * * question: * * Line 0 * * Word 9 *
* When he himself might his * * quietus make * * Line 19 * * Word 5 *
* And makes us * * rather bear those ills we have * * Line 25 * * Word 3 *
* With this * * regard their currents turn awry, * * Line 31 * * Word 2 *
* Be all my sins * * remember'd. * * Line 34 * * Word 4 *
* And thus the native hue of * * resolution * * Line 28 * * Word 6 *
* Must give us pause: there's the * * respect * * Line 12 * * Word 6 *
* No traveller * * returns, puzzles the will * * Line 24 * * Word 2 *
* To sleep: perchance to dream: ay, there's the * * rub; * * Line 9 * * Word 8 *
* No more; and by a sleep to * * say we end * * Line 5 * * Word 7 *
* For who would bear the whips and * * scorns of time, * * Line 14 * * Word 7 *
* Or to take arms against a * * sea of troubles, * * Line 3 * * Word 6 *
* The heart-ache and the thousand natural * * shocks * * Line 6 * * Word 6 *
* When we have * * shuffled off this mortal coil, * * Line 11 * * Word 3 *
* Is * * sicklied o'er with the pale cast of thought, * * Line 29 * * Word 1 *
* Be all my * * sins remember'd. * * Line 34 * * Word 3 *
* For in that * * sleep of death what dreams may come * * Line 10 * * Word 3 *
* No more; and by a * * sleep to say we end * * Line 5 * * Word 5 *
* To * * sleep: perchance to dream: ay, there's the rub; * * Line 9 * * Word 1 *
* And by opposing end them? To die: to * * sleep; * * Line 4 * * Word 8 *
* Devoutly to be wish'd. To die, to * * sleep; * * Line 8 * * Word 7 *
* The * * slings and arrows of outrageous fortune, * * Line 2 * * Word 1 *
* That makes calamity of * * so long life; * * Line 13 * * Word 4 *
* And lose the name of action. - * * Soft you now! * * Line 32 * * Word 7 *
* But that the dread of * * something after death, * * Line 22 * * Word 5 *
* The insolence of office and the * * spurns * * Line 17 * * Word 6 *
* Whether 'tis nobler in the mind to * * suffer * * Line 1 * * Word 7 *
* To grunt and * * sweat under a weary life, * * Line 21 * * Word 3 *
* Or to * * take arms against a sea of troubles, * * Line 3 * * Word 2 *
* That patient merit of the unworthy * * takes, * * Line 18 * * Word 6 *
* * * Than fly to others that we know not of? * * Line 26 * * Word 0 *
* * * That flesh is heir to, 'tis a consummation * * Line 7 * * Word 0 *
* To be, or not to be: * * that is the question: * * Line 0 * * Word 6 *
* * * That makes calamity of so long life; * * Line 13 * * Word 0 *
* * * That patient merit of the unworthy takes, * * Line 18 * * Word 0 *
* For in * * that sleep of death what dreams may come * * Line 10 * * Word 2 *
* But * * that the dread of something after death, * * Line 22 * * Word 1 *
* Than fly to others * * that we know not of? * * Line 26 * * Word 4 *
* But that * * the dread of something after death, * * Line 22 * * Word 2 *
* * * The fair Ophelia! Nymph, in thy orisons * * Line 33 * * Word 0 *
* * * The heart-ache and the thousand natural shocks * * Line 6 * * Word 0 *
* * * The insolence of office and the spurns * * Line 17 * * Word 0 *
* The pangs of despised love, * * the law's delay, * * Line 16 * * Word 5 *
* Whether 'tis nobler in * * the mind to suffer * * Line 1 * * Word 4 *
* And lose * * the name of action. - Soft you now! * * Line 32 * * Word 2 *
* And thus * * the native hue of resolution * * Line 28 * * Word 2 *
* * * The oppressor's wrong, the proud man's contumely, * * Line 15 * * Word 0 *
* Is sicklied o'er with * * the pale cast of thought, * * Line 29 * * Word 4 *
* * * The pangs of despised love, the law's delay, * * Line 16 * * Word 0 *
* The oppressor's wrong, * * the proud man's contumely, * * Line 15 * * Word 3 *
* To be, or not to be: that is * * the question: * * Line 0 * * Word 8 *
* Must give us pause: there's * * the respect * * Line 12 * * Word 5 *
* To sleep: perchance to dream: ay, there's * * the rub; * * Line 9 * * Word 7 *
* * * The slings and arrows of outrageous fortune, * * Line 2 * * Word 0 *
* The insolence of office and * * the spurns * * Line 17 * * Word 5 *
* The heart-ache and * * the thousand natural shocks * * Line 6 * * Word 3 *
* * * The undiscover'd country from whose bourn * * Line 23 * * Word 0 *
* That patient merit of * * the unworthy takes, * * Line 18 * * Word 4 *
* For who would bear * * the whips and scorns of time, * * Line 14 * * Word 4 *
* No traveller returns, puzzles * * the will * * Line 24 * * Word 4 *
* With this regard * * their currents turn awry, * * Line 31 * * Word 3 *
* And by opposing end * * them? To die: to sleep; * * Line 4 * * Word 4 *
* Must give us pause: * * there's the respect * * Line 12 * * Word 4 *
* To sleep: perchance to dream: ay, * * there's the rub; * * Line 9 * * Word 6 *
* When we have shuffled off * * this mortal coil, * * Line 11 * * Word 5 *
* With * * this regard their currents turn awry, * * Line 31 * * Word 1 *
* And makes us rather bear * * those ills we have * * Line 25 * * Word 5 *
* Is sicklied o'er with the pale cast of * * thought, * * Line 29 * * Word 8 *
* The heart-ache and the * * thousand natural shocks * * Line 6 * * Word 4 *
* * * Thus conscience does make cowards of us all; * * Line 27 * * Word 0 *
* And * * thus the native hue of resolution * * Line 28 * * Word 1 *
* The fair Ophelia! Nymph, in * * thy orisons * * Line 33 * * Word 5 *
* For who would bear the whips and scorns of * * time, * * Line 14 * * Word 9 *
* Devoutly * * to be wish'd. To die, to sleep; * * Line 8 * * Word 1 *
* * * To be, or not to be: that is the question: * * Line 0 * * Word 0 *
* To be, or not * * to be: that is the question: * * Line 0 * * Word 4 *
* Devoutly to be wish'd. * * To die, to sleep; * * Line 8 * * Word 4 *
* And by opposing end them? * * To die: to sleep; * * Line 4 * * Word 5 *
* To sleep: perchance * * to dream: ay, there's the rub; * * Line 9 * * Word 3 *
* * * To grunt and sweat under a weary life, * * Line 21 * * Word 0 *
* Than fly * * to others that we know not of? * * Line 26 * * Word 2 *
* No more; and by a sleep * * to say we end * * Line 5 * * Word 6 *
* * * To sleep: perchance to dream: ay, there's the rub; * * Line 9 * * Word 0 *
* And by opposing end them? To die: * * to sleep; * * Line 4 * * Word 7 *
* Devoutly to be wish'd. To die, * * to sleep; * * Line 8 * * Word 6 *
* Whether 'tis nobler in the mind * * to suffer * * Line 1 * * Word 6 *
* Or * * to take arms against a sea of troubles, * * Line 3 * * Word 1 *
* That flesh is heir * * to, 'tis a consummation * * Line 7 * * Word 4 *
* No * * traveller returns, puzzles the will * * Line 24 * * Word 1 *
* Or to take arms against a sea of * * troubles, * * Line 3 * * Word 8 *
* With this regard their currents * * turn awry, * * Line 31 * * Word 5 *
* To grunt and sweat * * under a weary life, * * Line 21 * * Word 4 *
* The * * undiscover'd country from whose bourn * * Line 23 * * Word 1 *
* That patient merit of the * * unworthy takes, * * Line 18 * * Word 5 *
* Thus conscience does make cowards of * * us all; * * Line 27 * * Word 6 *
* Must give * * us pause: there's the respect * * Line 12 * * Word 2 *
* And makes * * us rather bear those ills we have * * Line 25 * * Word 2 *
* No more; and by a sleep to say * * we end * * Line 5 * * Word 8 *
* And makes us rather bear those ills * * we have * * Line 25 * * Word 7 *
* When * * we have shuffled off this mortal coil, * * Line 11 * * Word 1 *
* Than fly to others that * * we know not of? * * Line 26 * * Word 5 *
* To grunt and sweat under a * * weary life, * * Line 21 * * Word 6 *
* For in that sleep of death * * what dreams may come * * Line 10 * * Word 6 *
* * * When he himself might his quietus make * * Line 19 * * Word 0 *
* * * When we have shuffled off this mortal coil, * * Line 11 * * Word 0 *
* * * Whether 'tis nobler in the mind to suffer * * Line 1 * * Word 0 *
* For who would bear the * * whips and scorns of time, * * Line 14 * * Word 5 *
* For * * who would bear the whips and scorns of time, * * Line 14 * * Word 1 *
* With a bare bodkin? * * who would fardels bear, * * Line 20 * * Word 4 *
* The undiscover'd country from * * whose bourn * * Line 23 * * Word 4 *
* No traveller returns, puzzles the * * will * * Line 24 * * Word 5 *
* Devoutly to be * * wish'd. To die, to sleep; * * Line 8 * * Word 3 *
* * * With a bare bodkin? who would fardels bear, * * Line 20 * * Word 0 *
* Is sicklied o'er * * with the pale cast of thought, * * Line 29 * * Word 3 *
* * * With this regard their currents turn awry, * * Line 31 * * Word 0 *
* For who * * would bear the whips and scorns of time, * * Line 14 * * Word 2 *
* With a bare bodkin? who * * would fardels bear, * * Line 20 * * Word 5 *
* The oppressor's * * wrong, the proud man's contumely, * * Line 15 * * Word 2 *
* And lose the name of action. - Soft * * you now! * * Line 32 * * Word 8 *
************************************************* ****************************************************** *********** **********
Process returned 0 (0x0) execution time : 6.666 s
Press any key to continue.
Reference
Koenig, Andrew & Moo, Barbara E., Accelerated C++, Addison-Wesley, 2000