Exercise 2-8
Write a program to generate the product of the numbers in the range [1,10).
Solution
The question asks as to compute the product of the numbers within the asymmetric range [1,10). In other words, the product of numbers within the range of 1 to 10, excluding 10. i.e.
1 x 2 x 3 ... x 7 x 8 x 9
Observation: this is the same as 9 factorial (9!). This is the same logic as computing n factorial.
Here outlines my solution strategy at the top level.
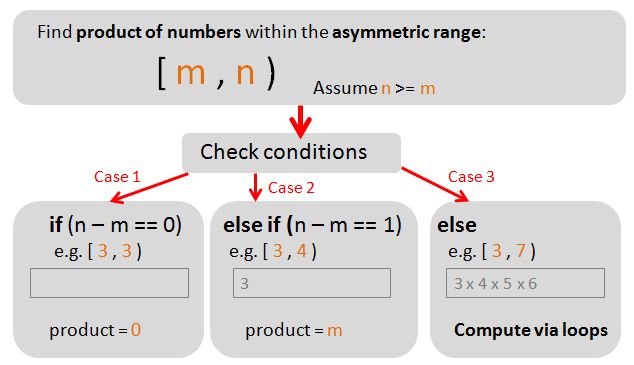
Descriptions:
- Fact: the product of 3 x 4 x 5 (ascending syntax) is the same as 5 x 4 x 3 (descending syntax). So for simplicity, we restrict ourself by only writing in an ascending syntax. i.e. use [3,6), and avoid [5,1) . This is the same as making the assumption of n >= m.
- Fact: Case 1, if (n-m)=0, e.g. the asymmetric range is [3,3), this is equivalent of saying the range is between 3 and 3 (excluding 3). Because this range is null, the product is also null (zero). No loops required.
- Fact: Case 2, if (n-m)=1, e.g. the asymmetric range is [3,4), this is equivalent of saying the range is between 3 and 4 (excluding 4). The range is therefore just the number 3 (i.e. m). Likewise, the product is also 3 (i.e. m). No loops required.
- Fact: Case 3, if (n-m)>=1, e.g. the asymmetric range is [3,7), this is equivalent of saying the range is between 3 and 7 (excluding 7). i.e. we are looking for the product of 3 x 4 x 5 x 6. To compute this we must use loops. The main focus of this post is case 3.
Case 3 Solution Strategy
After spending an entire Sunday afternoon on this question, I eventually spotted a pattern which I believe is consistent and can be leveraged in the forming of our algorithm. To demonstrate this pattern, I have put together some diagrams in PowerPoint and presented as snapshot images below. For clarity, we are going to focus on this particular (arbitrary) asymmetric range as our core example: [3, 7).
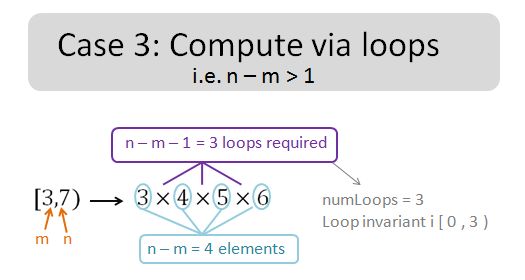
Observations:
- The number of elements is always (n-m). there are 4 elements in this case.
- The number of loops required is always (n-m-1). We need 3 loops in this case. (numLoops = 3).
- The number of loops required also equals to the number of (multiplication) operator.
- Knowing the number of loops required enable us to form the loop invariant i [0,numLoops).
Now, let’s try and observe more patterns – what happens at each loop? (See diagram below)
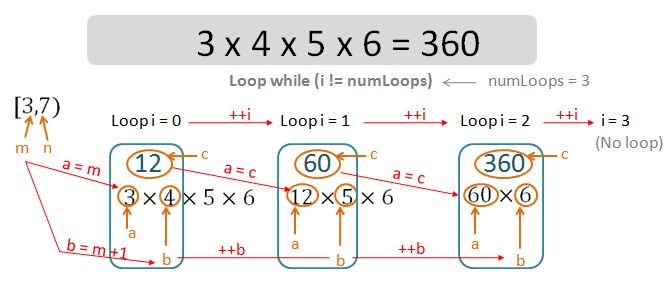
Observations:
- 4 major variables are required.
- The integer invariant i that controls whether the loop is to go ahead or terminate.
- The integer variable a – the lower number of the product (a x b).
- The integer variable b – the higher number of the product (a x b).
- The integer variable c – the product of (a x b).
- At the beginning of the very first loop, initialise values of a and b.
- At the end of each loop, the re-initialise values of a and b.
The final product of [m,n) is the value of c at the end of the very last loop.
For completeness, let’s do a drill down into the loops in greater depth. Bear in mind that for [3,7), the numLoops is n-m-1=3. We need 3 loops. The loop go ahead if the invariant i has not reached numLoops – it starts at 0 (zero), and get increment by 1 at end of each loop.
Invariant i = 0 (Loop)
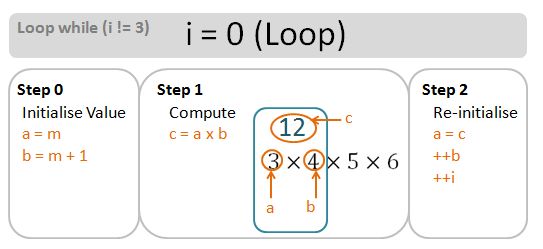
Invariant i = 1 (Loop)
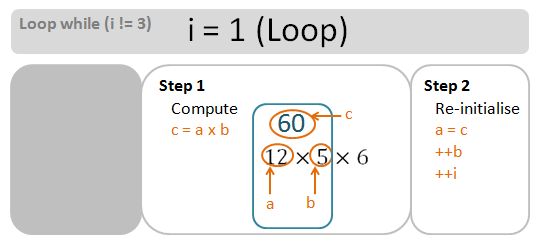
Invariant i = 2 (Loop)
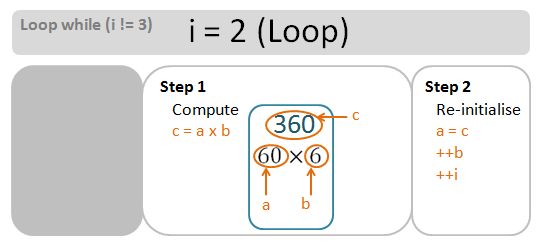
Invariant i = 3 (No Loop)

At the end of the loop, output the final result. The product of the numbers within the asymmetric range [m,n) is the value of c at the end of the very last loop. The following table summarises this looping process.
| Invariant i | a | b | c |
| 0 | 3 | 4 | 12 |
| 1 | 12 | 5 | 60 |
| 2 | 60 | 6 | 360 |
Full Program
We should now have all the fundamentals in the making of our program. This is my version of the program. (There are many ways to do this however!)
#include <iostream>
using namespace std;
int main()
{
cout << "***********************************************************\n"
<< "*** This program computes the product of the numbers ***\n"
<< "*** in the asymmetric range [m,n). ***\n"
<< "*** (Limitation: please ensure m is not larger than n) ***\n"
<< "*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***\n"
<< "***********************************************************";
cout << endl;
// Ask user to supply the startNumber
cout << "Enter m: ";
int m;
cin >> m;
// Ask user to supply the endNumber
cout << "Enter n: ";
int n;
cin >> n;
// Algorithm to compute the product of numbers within the asymmetric range [m,n)
const int startNumber = m ;
const int endNumber = n;
const int numElements = endNumber - startNumber;
const int numLoops = numElements - 1;
int c;
if (numElements == 0)
{c = 0;}
else if (numElements == 1)
{c = startNumber;}
else
{
int a = startNumber;
int b = startNumber + 1;
cout << " i, a, b, c " << endl;
for (int i = 0; i != numLoops; ++i)
{
c = a * b;
cout << i << ", " << a << ", " << b << ", " << c << endl;
a = c;
++b;
}
}
cout << "Asymmetric range: [" << startNumber << "," << endNumber << ")" << endl;
cout << "Number of elements: " << numElements << endl;
cout << "Number of loops required: " << numLoops << endl;
cout << "Product of numbers within the asymmetric range = " << c << endl;
return 0;
}
Result
The program is meant to be robust and be able to deal with any asymmetric range [m,n) as long as (n>=m). Case 1-3 are mainly for prove of concepts. Case 4 is the solution to the question (find product of numbers within the range [1,10).
- Case 1 – when (n-m)=0. e.g. [3,3)
- Case 2 – when (n-m)=1. e.g. [3,4)
- Case 3 – when (n-m)>1. e.g. [3,7)
- Case 4 – when (n-m)>1. e.g. [1,10)
Case 1 – Asymmetric Range [3,3)
*********************************************************** *** This program computes the product of the numbers *** *** in the asymmetric range [m,n). *** *** (Limitation: please ensure m is not larger than n) *** *** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) *** *********************************************************** Enter m: 3 Enter n: 3 Asymmetric range: [3,3) Number of elements: 0 Number of loops required: 0 Product of numbers within the asymmetric range = 0
Case 2 – Asymmetric Range [3,4)
*********************************************************** *** This program computes the product of the numbers *** *** in the asymmetric range [m,n). *** *** (Limitation: please ensure m is not larger than n) *** *** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) *** *********************************************************** Enter m: 3 Enter n: 4 Asymmetric range: [3,4) Number of elements: 1 Number of loops required: 0 Product of numbers within the asymmetric range = 3
Case 3 – Asymmetric Range [3,7)
*********************************************************** *** This program computes the product of the numbers *** *** in the asymmetric range [m,n). *** *** (Limitation: please ensure m is not larger than n) *** *** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) *** *********************************************************** Enter m: 3 Enter n: 7 i, a, b, c 0, 3, 4, 12 1, 12, 5, 60 2, 60, 6, 360 Asymmetric range: [3,7) Number of elements: 4 Number of loops required: 3 Product of numbers within the asymmetric range = 360
Case 4- Asymmetric Range [1,10)
*********************************************************** *** This program computes the product of the numbers *** *** in the asymmetric range [m,n). *** *** (Limitation: please ensure m is not larger than n) *** *** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) *** *********************************************************** Enter m: 1 Enter n: 10 i, a, b, c 0, 1, 2, 2 1, 2, 3, 6 2, 6, 4, 24 3, 24, 5, 120 4, 120, 6, 720 5, 720, 7, 5040 6, 5040, 8, 40320 7, 40320, 9, 362880 Asymmetric range: [1,10) Number of elements: 9 Number of loops required: 8 Product of numbers within the asymmetric range = 362880
Compute the N factorial
Note that this program may also be used as a skeleton program for computing factorial. e.g. 5! = 1 x 2 x 3 x 4 x 5. In other words, to compute n! this is effectively the same as computing the internal product of the numbers within the asymmetric range (0, n+1).
Conclusion
The product of the numbers within the asymmetric range [0,10) is 362880, as computed by the program (and verified by calculators). This program might also be used as a skeleton program for computing factorial.
Thank you so much. Appreciated!
Hi there ! Did you do the rest of the cases just for fun ?
Because I think the program for computing product of [1,10) is quite straightforward.
Thanks!