Exercise 7-9
(difficult) The implementation of nrand in S7.4.4/135 will not work for arguments greater than RAND_MAX. Usually, this restriction is no problem, because RAND_MAX is often the largest possible integer anyway. Nevertheless, there are implementations under which RAND_MAX is much smaller than the largest possible integer. For example, it is not uncommon for RAND_MAX to be 32767 (2^15 -1) and the largest possible integer to be 2147483647 (2^31 -1). Reimplement nrand so that it works well for all values of n.
Solution
This exercise is great – it gives us the chance to create and understand an algorithm that generate random number beyond RAND_MAX (the largest default C++ random number that can be “reached” by the rand() function) whilst ensuring even probability distribution of that random number (i.e. the number “10” having the same chance of getting picked as the number “234”, etc.).
Andrew and Barbara (the authors) provided the original code for this exercise on GitHub here back in year 2000. I took the liberty to read through it with the aim of understanding and making sense of the solution. After 3 evenings of sketching diagrams in my notepad (and getting stuck multiple times), I eventually understood the underlying principle / concepts, and managed to come up with an algorithm built on the authors’ original solution (with slight differences).
In this post I shall illustrate the derivation and implementation of the algorithm (which I can actually visualise). I use PowerPoint to draw out some diagrams to aid visualising the algorithms. I would like to express my sincerest thanks to Andrew and Barbara for this very wonderful exercise.
What Will Our nrand() Do?
We are going to create a function nrand() that returns a random integer, given the asymmetric range [0, randomOutcomeLimit).
e.g. if randomOutcomeLimit is 4, then the randomOutcome may be either 0, 1, 2, 3 – each with an equal (25%) chance of getting picked.
Terminologies
Before going any further, I believe it is a good idea to define some core variables / terminologies.
- randomDriver: this is essentially rand(). The C++ default (seeding) random number that span within the asymmetric range [0, randomDriverLimit). We use randomDriver to “drive” (or compute) the eventual randomOutcome.
- randomDriverLimit: this is RAND_MAX + 1. i.e. “one-above” the maximum possible randomDriver value.
- randomOutcome: this is the random number that gets returned. It spans within the symmetric range [0, randomOutcomeLimit). The algorithm ensures that every single randomOutcome has the same probability of getting randomly selected. The randomOutcome is “driven” (or determined) by the randomDriver.
- randomOutcomeLimit: “one-above” the maximum possible randomOutcome value.
- bucketSize: this is “the glue” between randomDriver and randomOutcome. Think of it as the ratio between the two. To enable us to translate a randomDriver into a randomOutcome (and vice versa).
- remainder: this is used in the computation of randomOutcome. Only relevant for the case whhen randomOutcomeLimit > randomDriverLimit.
Note: in the “pseudo diagrams” that I have drawn up in PowerPoint, I shall use RD to represent randomDriver, and RO to represent randomOutcome.
Algorithm
The algorithm for nrand() will cater for two scenarios:
- Case 1: when randomOutcomeLimit <= randomDriverLimit
- Case 2: when randomOutcomeLimit > randomDriverLimit
It may be easier if I display the complete nrand.cpp code here now, and walk through in more details afterwards.
The nrand.cpp Code
#include <cmath> // ceil
#include <cstdlib> // rand, RAND_MAX, srand
#include <stdexcept> // domain_error
using std::ceil;
using std::rand;
using std::domain_error;
// Asymmetric ranges:
// randomOutcome: [0, randomOutcomeLimit)
// randomDriver: [0, randomDriverLimit)
int nrand(int randomOutcomeLimit) {
if (randomOutcomeLimit <= 0)
throw domain_error("Argument to nrand is out of range");
int randomOutcome;
int randomDriverLimit = RAND_MAX + 1;
if (randomOutcomeLimit <= randomDriverLimit) {
const int bucketSize = randomDriverLimit / randomOutcomeLimit;
do {
int bucket = rand() / bucketSize;
randomOutcome = bucket;
} while (randomOutcome >= randomOutcomeLimit);
} else {
const int bucketSize = ceil(randomOutcomeLimit / randomDriverLimit);
do {
int bucket = nrand(randomDriverLimit);
int remainder = nrand(bucketSize);
randomOutcome = (bucket * bucketSize) + remainder;
} while (randomOutcome >= randomOutcomeLimit);
}
return randomOutcome;
}
Case 1: when randomOutcomeLimit <= randomDriverLimit
if (randomOutcomeLimit <= randomDriverLimit) {
const int bucketSize = randomDriverLimit / randomOutcomeLimit;
do {
int bucket = rand() / bucketSize;
randomOutcome = bucket;
} while (randomOutcome >= randomOutcomeLimit);
}
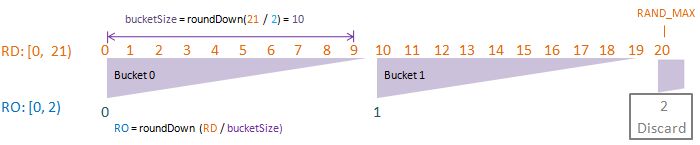
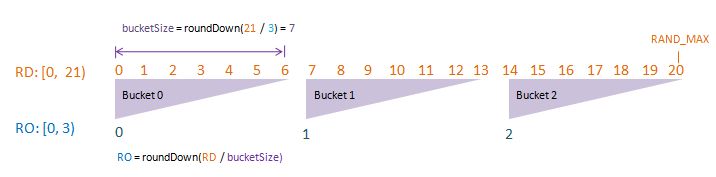
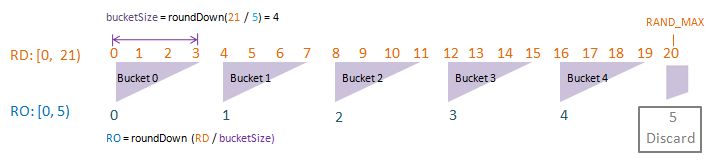
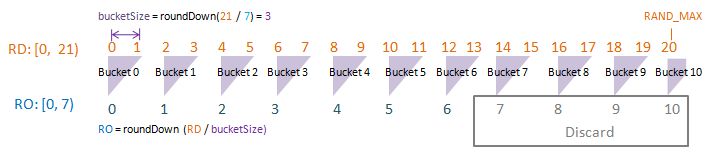
Since the values of randomOutcomeLimit and randomDriverLimit are pre-defined, we compute our bucketSize by taking the ratio between the two. We use the randomDriverlimit as the numerator (and randomDriverLimit as the denominator) to ensure this ratio is a non-fraction. Think of bucketSize as: “The number of randomDrivers per randomOutcome”. 10 randomDrivers per randomOutcome makes sense. 0.5 randomDrivers per randomOutcome does not.
Note that the equation automatically “round-down” the ratio to the integer (instead of “round-up”). This is to ensure every single randomOutcome to have the same probability of being picked.
To illustrate this, assume we have randomDriverLimit = 5 (i.e. RAND_MAX = 4. i.e. randomDriver may be 0, 1, 2, 3.), and randomOutcomeLimit = 2 (i.e. randomOutcome maybe 0 and 1).
Compute bucketSize With “Round-down” (desirable)
In the case of computing bucketSize using “round-down”, the probability distribution of randomOutcome is even. This is what we want in a random number generator.
Compute bucketSize With “Round-up” (Un-desirable)
In the case of computing bucketSize using “round-up”, the probability distribution of randomOutcome is non-even. This is what we DO NOT want in a random number generator.
Further Visualisation
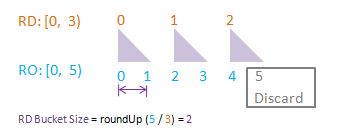
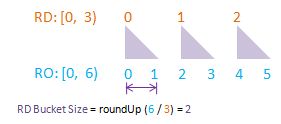
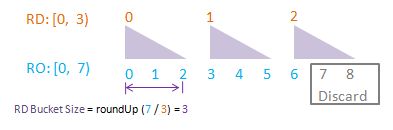
To visualise randomDriver, randomDriverLimit, randomOutcome, randomOutcomeLimit, bucket, and bucketSize all in one go, I have put together some PowerPoint diagrams here which I believe will speak for themselves without the need of much further (wordy) explanations! I assume a fixed randomDriverLimit of 21, and vary the randomOutcomeLimit for illustrations.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 2.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 3.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 4.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 5.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 6.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 7.
Visualise: randomDriverLimit of 21, randomOutcomeLimit = 11.
Case 2: when randomOutcomeLimit > randomDriverLimit
} else {
const int bucketSize = ceil(randomOutcomeLimit / randomDriverLimit);
do {
int bucket = nrand(randomDriverLimit);
int remainder = nrand(bucketSize);
randomOutcome = (bucket * bucketSize) + remainder;
} while (randomOutcome >= randomOutcomeLimit);
}
We compute bucketSize in a similar manner as Case 1, except that we use “round-up” (i.e. using the “ceil” function in C++) instead of “round-down”. We also ensure a non-fraction bucketSize (as explained in Case 1), by putting randomOutcomeLimit as the numerator, and randomDriverLimit as the denominator. Think of bucketSize as: “The number of randomOutcome per randomDriver”. 10 randomOutcomes per randomRandomDriver makes sense. 0.5 randomOutcome per randomRandomDriver does not.
We use “round-up” in the computation of the bucketSize to ensure the entire range of randomDriver can “cover” the entire range of randomOutcome. I can illustrate this point easily via some diagrams as followings.
In addition, we use nrand recursively downstream. Unfortunately I am not able to explain this bit in words. I would however recommend to look at the diagrams in the following section – looking at these diagrams have helped in understanding how the remaining steps hang together. I hope you may be able to figure this out for yourself too! (use the diagrams!).
Compute bucketSize With “Round-down” (un-desirable)
Compute bucketSize With “Round-up” (desirable)
Further Visualisation
To visualise randomDriver, randomDriverLimit, randomOutcome, randomOutcomeLimit, bucket, and bucketSize all in one go, I have put together some PowerPoint diagrams here which I believe will speak for themselves without the need of much further (wordy) explanations! I assume a fixed randomDriverLimit of 2, and vary the randomOutcomeLimit for illustrations.
Visualise: randomDriverLimit of 2, randomOutcomeLimit = 5.
Visualise: randomDriverLimit of 2, randomOutcomeLimit = 6.
Visualise: randomDriverLimit of 2, randomOutcomeLimit = 7.
Visualise: randomDriverLimit of 3, randomOutcomeLimit = 5.
Visualise: randomDriverLimit of 3, randomOutcomeLimit = 6.
Visualise: randomDriverLimit of 3, randomOutcomeLimit = 7.
The Project
To wrap up the entire projects I shall document the C++ header and source files here. The nrand algorithm aims to generate random numbers within the range [0, randomOutcomeLimit) in an even probability distribution – i.e. each random outcome has the same chance of being picked.
Source File List
Header File List
Source Files
main.cpp
#include <iostream> // std::cout, std::cin, std::endl
#include <cstdlib> // RAND_MAX, srand
#include <ctime> // std::time
#include "nrand.h" // nrand
using std::cout;
using std::cin;
using std::endl;
using std::srand;
using std::time;
int main()
{
// Uncomment this line to see new randomness every time the job is run.
srand(time(NULL));
// Generate random numbers within the range [0, n)
const int n = 999999999; // try n = 10, and n = 3276700
const int numbersPerLine = 5;
// Display the limits
cout << "randomOutcomeLimit: " << n << endl;
cout << "randomDriverLimit: " << (RAND_MAX + 1) << endl;
// Display the randomOutcomes
for (int i = 0; i != 100; ++i) {
if (i == 0)
cout << nrand(n);
else {
cout << ", " << nrand(n);
// start a new line
if (i != 0 && (i+1) % numbersPerLine == 0)
cout << endl;
}
}
return 0;
}
nrand.cpp
#include <cmath> // ceil
#include <cstdlib> // rand, RAND_MAX, srand
#include <stdexcept> // domain_error
using std::ceil;
using std::rand;
using std::domain_error;
// Asymmetric ranges:
// randomOutcome: [0, randomOutcomeLimit)
// randomDriver: [0, randomDriverLimit)
int nrand(int randomOutcomeLimit) {
if (randomOutcomeLimit <= 0)
throw domain_error("Argument to nrand is out of range");
int randomOutcome;
int randomDriverLimit = RAND_MAX + 1;
if (randomOutcomeLimit <= randomDriverLimit) {
const int bucketSize = randomDriverLimit / randomOutcomeLimit;
do {
int bucket = rand() / bucketSize;
randomOutcome = bucket;
} while (randomOutcome >= randomOutcomeLimit);
} else {
const int bucketSize = ceil(randomOutcomeLimit / randomDriverLimit);
do {
int bucket = nrand(randomDriverLimit);
int remainder = nrand(bucketSize);
randomOutcome = (bucket * bucketSize) + remainder;
} while (randomOutcome >= randomOutcomeLimit);
}
return randomOutcome;
}
Header Files
nrand.h
#ifndef GUARD_NRAND_H #define GUARD_NRAND_H // nrand.h int nrand(int); #endif // GUARD_NRAND_H
Test Result
Test Case 1: when randomOutcomeLimit > randomDriverLimit
Set randomOutcomeLimit (i.e. the “n” in the main program) = 10. (randomDriverLimit on my Windows Vista System is 32768. i.e. RAND_MAX = 32767).
randomOutcomeLimit: 10 randomDriverLimit: 32768 0, 7, 3, 4, 5 , 2, 3, 5, 7, 8 , 5, 1, 0, 9, 1 , 0, 1, 2, 5, 3 , 1, 3, 5, 9, 1 , 8, 4, 8, 8, 8 , 2, 6, 8, 1, 4 , 5, 4, 5, 7, 4 , 7, 5, 1, 2, 0 , 5, 7, 3, 6, 9 , 8, 6, 5, 6, 4 , 4, 3, 2, 2, 5 , 9, 3, 0, 2, 7 , 8, 8, 1, 7, 1 , 4, 2, 3, 0, 0 , 8, 1, 2, 5, 9 , 4, 2, 5, 9, 9 , 7, 4, 3, 0, 4 , 9, 5, 6, 8, 0 , 4, 1, 6, 5, 2 Process returned 0 (0x0) execution time : 0.293 s Press any key to continue.
Test Case 2: when randomOutcomeLimit <= randomDriverLimit
Set randomOutcomeLimit (i.e. the “n” in the main program) = 999999999. (randomDriverLimit on my Windows Vista System is 32768. i.e. RAND_MAX = 32767).
randomOutcomeLimit: 999999999 randomDriverLimit: 32768 40716497, 545497019, 401935189, 573265717, 87747530 , 675712555, 451019252, 549144813, 442862664, 914580320 , 3346215, 284749221, 212065917, 568356864, 979714558 , 544197549, 418473188, 720009720, 433822531, 424721581 , 541414236, 257758341, 608087599, 83473957, 984179693 , 492106188, 331214530, 521536020, 935375395, 580651497 , 195237728, 664468742, 414572965, 645131011, 682450472 , 477285531, 969901982, 319040147, 723433358, 897986272 , 120072600, 13688281, 426975024, 332152250, 774858930 , 85086071, 749114164, 49610236, 923599508, 602891952 , 599691044, 621946048, 156375628, 885810442, 918023686 , 135602107, 449128117, 661074165, 86314758, 699792585 , 461395423, 916830653, 398552621, 933505532, 326772882 , 142535635, 570358869, 573805944, 391791222, 527897950 , 942405333, 383272295, 777643889, 483575430, 421364976 , 808711544, 623226506, 83231569, 970354625, 918738412 , 272996097, 134992162, 663575905, 719215842, 172551438 , 345021838, 170806050, 154762077, 794127443, 949285447 , 81891829, 62877966, 418973269, 343240040, 888728945 , 627644733, 808847443, 814885588, 628243461, 188955197 Process returned 0 (0x0) execution time : 0.415 s Press any key to continue.