Tag Archives: numpy
NumPy Exercise – Argsort and Fancy Indexing
This post summarises my solution to this NumPy Fancy Indexing Exercise (Challenge 3) – originated from scipy-lectures.org
The Problem
Generate a 10 x 3 array of random numbers (in range [0,1]). For each row, pick the number closest to 0.5.
- Use
absandargsortto find the column j closest for each row. - Use fancy indexing to extract the numbers. (Hint:
a[i,j]– the arrayimust contain the row numbers corresponding to stuff inj.)
The Solution
First version code to illustrate how things work:
Now we know how things work, let’s compact the solution (optional).
Major Learning Summary
- Fancy Indexing –
a[rows, cols]ora[[1, 2, 3, 4], [2, 1, 0, 1]] - Sorting –
sort,argsort,argmin/argmax.
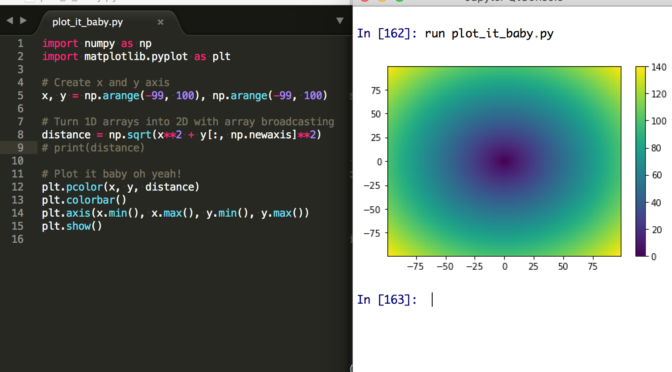
NumPy Array Broadcasting: Combine 1D arrays into 2D
This NumPy Array Broadcasting example is inspired by this SciPy Lecture Chapter on Array Broadcasting.
Code:
Note the use of y[:, np.newaxis].
Note also that this example might be made much simplier with np.ogrid and np.mgrid. (See the SciPy-Lectures chapter on broadcasting)
Python NumPy Advance Element Selection Trick – Slice and Jump
TL;DR
This visual example will show you how to a neatly select elements in a NumPy Matrix (2 dimensional array) in a pretty entertaining way (I promise).
(Caution: this is a NumPy array specific example with the aim of illustrating the a use case of “double colons” :: for jumping of elements in multiple axes. This example does not cover native Python data structures like List).
One concrete example to rule them all…
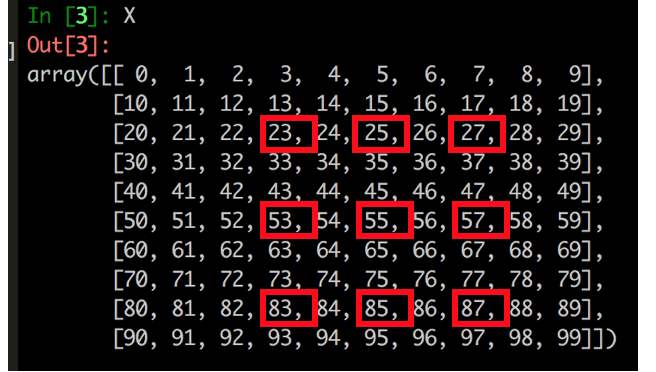
Say we have a NumPy matrix that looks like this:
In [1]: import numpy as np
In [2]: X = np.arange(100).reshape(10,10)
In [3]: X
Out[3]:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
[20, 21, 22, 23, 24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35, 36, 37, 38, 39],
[40, 41, 42, 43, 44, 45, 46, 47, 48, 49],
[50, 51, 52, 53, 54, 55, 56, 57, 58, 59],
[60, 61, 62, 63, 64, 65, 66, 67, 68, 69],
[70, 71, 72, 73, 74, 75, 76, 77, 78, 79],
[80, 81, 82, 83, 84, 85, 86, 87, 88, 89],
[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])
Say for some reason, your boss wants you to select the following elements:
“But How???”… Read on! (We can do this in a 2-step approach)
Step 1 – Obtain subset
Specify the “start index” and “end index” in both row-wise and column-wise directions.
In code:
In [5]: X2 = X[2:9,3:8]
In [6]: X2
Out[6]:
array([[23, 24, 25, 26, 27],
[33, 34, 35, 36, 37],
[43, 44, 45, 46, 47],
[53, 54, 55, 56, 57],
[63, 64, 65, 66, 67],
[73, 74, 75, 76, 77],
[83, 84, 85, 86, 87]])
Notice now we’ve just obtained our subset, with the use of simple start and end indexing technique. Next up, how to do that “jumping”… (read on!)
Step 2 – Select elements (with the “jump step” argument)
We can now specify the “jump steps” in both row-wise and column-wise directions (to select elements in a “jumping” way) like this:
In code (note the double colons):
In [7]: X3 = X2[::3, ::2]
In [8]: X3
Out[8]:
array([[23, 25, 27],
[53, 55, 57],
[83, 85, 87]])
We have just selected all the elements as required! :)
Consolidate Step 1 (start and end) and Step 2 (“jumping”)
Now we know the concept, we can easily combine step 1 and step 2 into one consolidated step – for compactness:
In [9]: X4 = X[2:9,3:8][::3,::2]
In [10]: X4
Out[10]:
array([[23, 25, 27],
[53, 55, 57],
[83, 85, 87]])
Done!
(I’ve also posted this trick in this Stackoverflow forum)