Exercise 4-0
Compile, execute, and test the programs in this chapter
Solution
Chapter 4 (Organising programs and data) contains a mix of all learnings gained from previous chapters (0 to 3), with the newly added introduction to program partitioning – to break down a large program into multiple .cpp (source) files and .h (header) files to make it more manageable. In this post I will demonstrate my understanding of chapter 4 via presenting the one core project which encompasses the use of program partitioning.
My learning strategy:
- Read through chapter 4 – try and understand as much as possible.
- Write and execute the chapter 4 project in Code::Block – try and get the partitioned program work.
- Read through chapter 4 again and experiment with the project – now that the project is working, I would like to understand why and how it works.
- Document core learning outcome – this is what this post is for!
Now that I have spent 2 days completing (and re-iterating) step 1 to 3 above, I believe it is time to execute step 4 above – to document learning outcome via writing this post.
The Project
Purpose of the Chapter 4 project: to read in a flat-file format like input, and produce a summarised output (see diagram below).

Chapter 4 requires us to create a partitioned program (or so called project) that is formed of multiple .cpp source files and .h header files. These files somewhat “know” about each other and can work together in the solving of big problem.
In Code::Block (or probably most of the mainstream IDE), we can create such a project fairly easily to keep these files tidy / organised.
I now document the C++ Source Files and Header Files in the following sections.
C++ Source Files
- main.cpp – this is the first program that is run during the implementation phase.
- grade.cpp – contains all functions relating to computing grades.
- median.cpp – contains all functions relating to computing median.
- Student_info.cpp – contains all functions relating to handling a Student_info object.
C++ Header Files
- grade.h – declare the functions as defined in grade.cpp
- median.h – declare the functions as defined in median.cpp
- Student_info.h – declare the functions as defined in Student_info.cpp, plus defining the data structure of the Student_info (object) type.
See my post How to add header and source files in Code::Block for additional information.
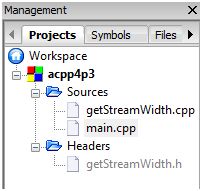
This diagram below shows what the Code::Block Management Tree look like after successful creation of these files.
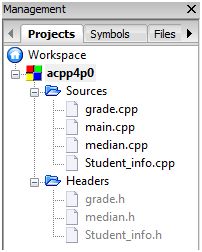
The actual content of the source and header files are documented in the following sections.
Source Files
main.cpp
#include <algorithm>
#include <iomanip>
#include <ios>
#include <iostream>
#include <stdexcept>
#include <string>
#include <vector>
#include "grade.h"
#include "Student_info.h"
using std::cin;
using std::cout;
using std::endl;
using std::domain_error;
using std::max;
using std::setprecision;
using std::sort;
using std::streamsize;
using std::string;
using std::vector;
int main()
{
vector<Student_info> students;
Student_info record;
string::size_type maxlen = 0; // the length of the longest name
// read and store all the student's data.
// Invariant: students contain all the student records read so far
// maxlen contains the length of the longest name in students
while (read(cin, record))
{
// find the length of longest name
maxlen = max(maxlen, record.name.size());
students.push_back(record);
}
// alphabetize the student records
sort(students.begin(), students.end(), compare);
// write the names and grades
for (vector<Student_info>::size_type i = 0;
i != students.size(); ++i)
{
//write the name, padded on teh right to maxlen + 1 characters
cout << students[i].name
<< string(maxlen + 1 - students[i].name.size(), ' ');
//compute and write the grade
try
{
double final_grade = grade(students[i]);
streamsize prec = cout.precision();
cout << setprecision(3) << final_grade
<< setprecision(prec);
}
catch (domain_error e)
{
cout << e.what();
}
cout << endl;
}
return 0;
}
grade.cpp
#include <stdexcept>
#include <vector>
#include "grade.h"
#include "median.h"
#include "Student_info.h"
using std::domain_error;
using std::vector;
// definitions for the grade functions from S4.1/52, S4.1.2/54, S4.2.2/63
// compute a student's overall grade from midterm and final exam
// grades and homework grade (S4.1/52)
double grade(double midterm, double final, double homework)
{
return 0.2 * midterm + 0.4 * final + 0.4 * homework;
}
// compute a student's overall grade from midterm and final exam grades
// and vector of homework grades.
// this function does not copy its argument, because median (function) does it for us.
// (S4.1.2/54)
double grade(double midterm, double final, const vector<double>& hw)
{
if (hw.size() == 0)
throw domain_error("student has done no homework");
return grade(midterm, final, median(hw));
}
// this function computes the final grade for a Student_info object
// (S4.2.2/63)
double grade(const Student_info& s)
{
return grade(s.midterm, s.final, s.homework);
}
// source file for the median function
#include <algorithm>
#include <stdexcept>
#include <vector>
using std::domain_error;
using std::sort;
using std::vector;
// compute the median of a vector<double>
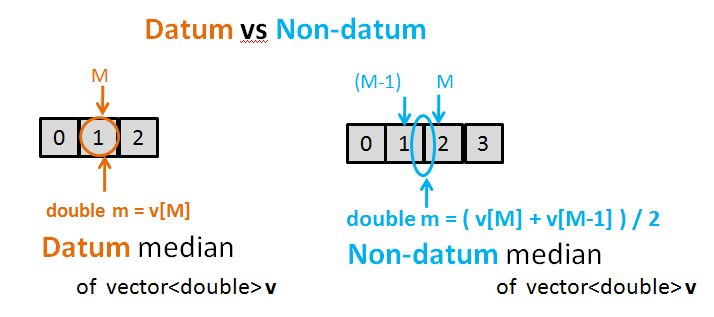
double median(vector<double> vec)
{
typedef vector<double>::size_type vec_sz;
vec_sz size = vec.size();
if (size == 0)
throw domain_error("median of an empty vector");
sort(vec.begin(),vec.end());
vec_sz mid = size/2;
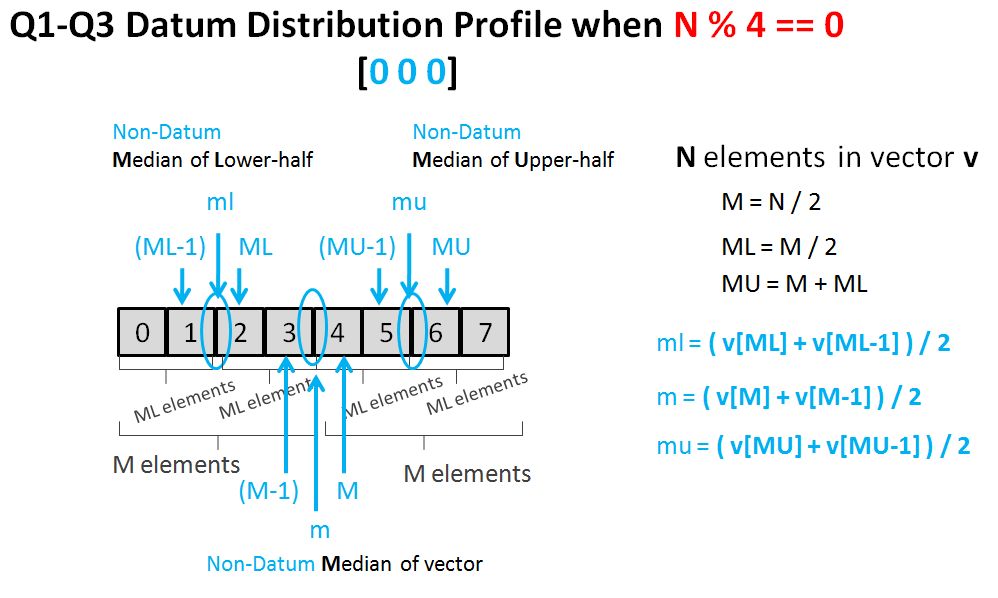
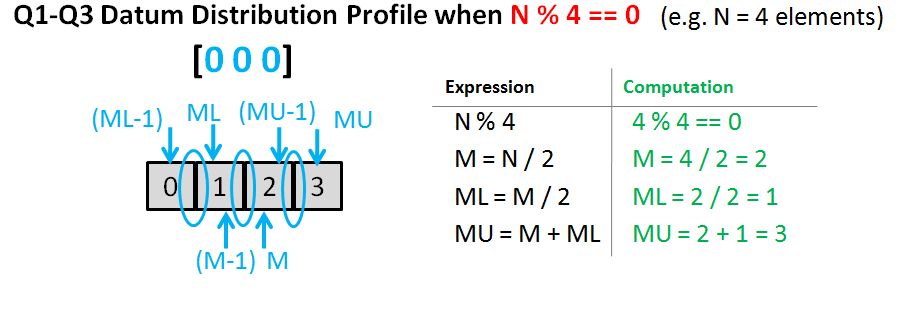
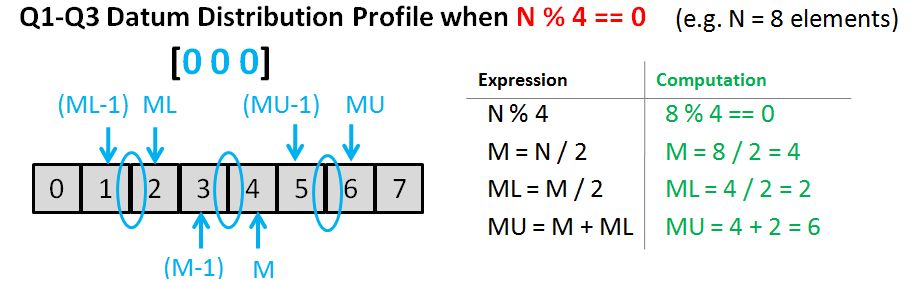
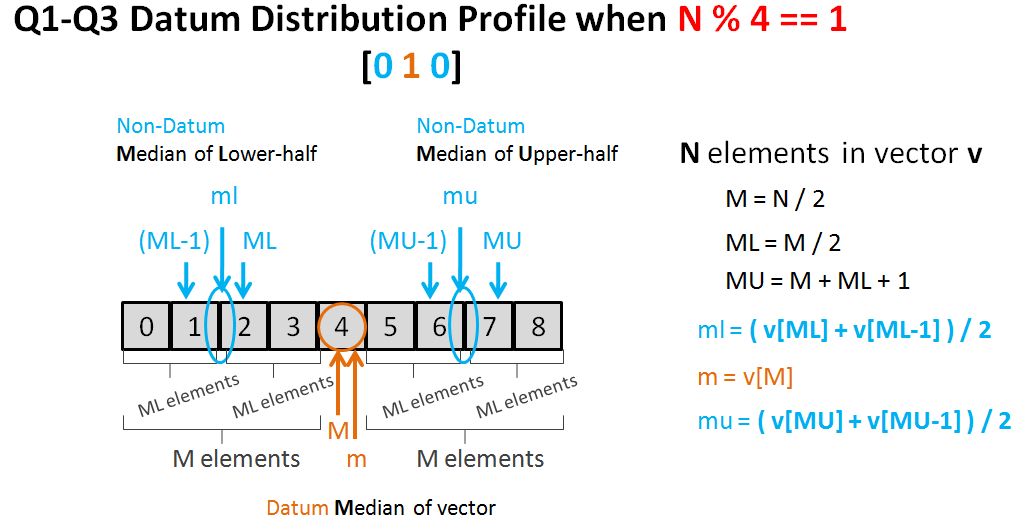
return size % 2 == 0 ? (vec[mid] + vec[mid-1]) / 2 : vec[mid];
}
Student_info.cpp
#include "Student_info.h"
using std::istream;
using std::vector;
// we are interested in sorting the Student_info object by the student's name
bool compare(const Student_info& x, const Student_info& y)
{
return x.name < y.name;
}
// read student's name, midterm exam grade, final exam grade, and homework grades
// and store into the Student_info object
// (as defined in S4.2.2/62)
istream& read(istream& is, Student_info& s)
{
// read and store the student's name and midterm and final exam grades
is >> s.name >> s.midterm >> s.final;
// read and store all the student's homework grades
read_hw(is, s.homework);
return is;
}
// read homework grades from an input stream into a vector<double>
// (as defined in S4.1.3/57)
istream& read_hw(istream& in, vector<double>& hw)
{
if (in)
{
// get rid of previous contents
hw.clear();
// read homework grades
double x;
while (in >> x)
hw.push_back(x);
// clear the stream so that input will work for the next student
in.clear();
}
return in;
}
Header Files
grade.h
#ifndef GUARD_GRADE_H
#define GUARD_GRADE_H
//grade.h
#include <vector>
#include "Student_info.h"
double grade(double, double, double);
double grade(double, double, const std::vector<double>&);
double grade(const Student_info&);
#endif // GUARD_GRADE_H
#ifndef GUARD_MEDIAN_H
#define GUARD_MEDIAN_H
// median.h - final version
#include <vector>
double median(std::vector<double>);
#endif // GUARD_MEDIAN_H
Student_info.h
#ifndef GUARD_STUDENT_INFO_H
#define GUARD_STUDENT_INFO_H
// Student_info.h
#include <iostream>
#include <string>
#include <vector>
struct Student_info
{
std::string name;
double midterm, final;
std::vector<double> homework;
};
bool compare(const Student_info&, const Student_info&);
std::istream& read(std::istream&, Student_info&);
std::istream& read_hw(std::istream&, std::vector<double>&);
#endif // GUARD_STUDENT_INFO_H
Test Program
I believe that by test running the program multiple times (and differently each time) it will enable me to understand a bit more about why and how the program works as a whole. Experiment, experiment, and experiment…
After compiling all the files followed by hitting the run program button, a blank command window fires up awaits me to provides input. I performed the various tests using different input values (or format). The results will hopefully enable me to visualise patterns and understand the program a bit more.
Test 1
I will now input all values in 1 line, hit enter, then hit end-of-file (F6), then hit end-of-file (F6) again. See what the output looks like and why it appears that way.
Test 1 – Input and Result
Johnny 70 80 50 60 30 Fred 95 90 100 100 100 Joe 40 40 50 60 50 70 70 50
^Z
^Z
Fred 95
Joe 46
Johnny 66
Process returned 0 (0x0) execution time : 121.246 s
Press any key to continue.
Test 1 – Observation and Explanation
- The first while (read(cin, record)) { } (within the main program) activates the std::cin which enables user the type-in input values via the console window.
- I type all values in one line (separated by a space character), like this: name, midterm score, final score, homework scores.
- I then hit the enter button to open up a new line. This “hitting the enter button” action parses the values that I typed, into a buffer.
- The istream& read(istream&, Student_info&) function (as defined in Student_info.cpp) parse the first buffer value “Johnny” to s.name, and clear that value from the buffer.
- It then parse the (now first) buffer value 70 to s.midterm, and clear that value from the buffer.
- It then parse the (now first) buffer value 80 to s.final, and clear that value from the buffer.
- The istream& read_hw(istream&, vector<double>&) function is then invoked (as defined in Student_info.cpp). It prepares an empty vector<double>& hw. The while (in >> x) parses all the valid values from the buffer to the (vector) hw, until the value become invalid (e.g. a string rather than a number). In this case, this procedure parses the 50, 60, and 30 to hw[0], hw[1], hw[2] respectively. When the procedure encounters the (non-numeric) value “Fred”, it exits the while automatically and change the status of the istream& in to an error status. The in.clear() reset the error status to enable smooth data parse for the next student. Because the “Fred” was not parsed during this while loop (as the while loop got exited due to non-numeric value), and therefore not cleared from the buffer, it now becomes the first value of the buffer (this is an important note to make – because in the 2nd loop, the program now able to parse “Fred” as a name of the 2nd Student_info object!).
- The while (read(cin, record)) { } then enters the 2nd loop (to process Fred’s scores). It then repeats in the 3rd loop to process Joe’s scores. In the end, the vector<Student_info> students contains the 3 Student_info objects (i.e. “Johnny”, “Fred”, and “Joe”)
- After processing the entirety of the one-liner input, I enter end-of-file button. This has the effect of exiting the while loop of read_hw function.
- I enter the enter end-of-file button once more time. This has the effect of exiting the while loop (of the main program).
- Now that both loops are exited, the main program then proceeds to the sort(students.begin(), students.end(), compare) phase. The downstream block of code output the result in a nicely formatted summary showing the overall score for each student, sorted by the student’s name.
The above explanation is not comprehensive, as to explain the whole program, it would take multiple pages! The main reason that I decided to document the above is to highlight these core observations / concepts:
- The behaviour of std::cin and buffer – my previous post Solution to Exercise 1-6 has enabled me to make sense of why and how this chapter 4 program works. e.g. the effect of hitting that enter button first time round!
- The first end-of-file exits the inner-most while loop (the one within the read_hw function).
- The second end-of-file exits the outer-most while loop (the one within the main program) – which enable the implementation to continue to the sort step (within the main program).
- Chapter 4 of the book has explained most of the details in depth – so I am not going to repeat here.
Test 2
I will now input in the most consistent and most understandable format. i.e. input the values 1 line per student (Name, mid-term score, final score, and homework scores). When I am done I will hit enter, then hit end-of-file (F6), then hit end-of-file (F6) again. See what the output looks like and why it appears that way. (I will use the same values as of test 1 – to hopefully prove that the output result would be the same as test 1.)
Test 2 – Input and Result
Johnny 70 80 50 60 30
Fred 95 90 100 100 100
Joe 40 40 50 60 50 70 70 50
^Z
^Z
Fred 95
Joe 46
Johnny 66
Process returned 0 (0x0) execution time : 33.322 s
Press any key to continue.
Test 2 – Observation and Explanation
The output of this test is exactly the same as test 1. This is not surprising. The overall process of test 2 is mostly similar to test 1, with one very minor difference: in test 1 we input all the values in 1 line and hit enter – this parses all values (for all 3 students) in the buffer. The downstream process then read from the buffer and proceed accordingly, and eventually created the 3 Student_info type objects.
In this test 2, we input the values for student 1 in 1 line. Hitting enter parse the values of this 1 student into the buffer. The read() function reads the name, then mid-term score, then the final score, then the read_hw function (within the read function) reads the vector elements homework 0 to home work 4. The implementation then awaits for our next homework score.
Then we type the values for the 2nd student (Fred) in a similar fashion. This time, after we hit the enter button to open up the 3rd line, the read_hw function (that we talked about just now) that is expecting a numeric homework 5, suddenly “sees” this non-numeric (string) value “Fred”. It exit the while loop (of the read_hw function), create an error status, then clear that error status as per the in.clear() (to enable smooth read of the next student). Going back to the main program, the 2nd while loop while (read(cin, record)) { } start reading that “Fred” (first value of the buffer) as the student’s name, followed by reading the renaming numeric values in the buffer (as mid-term score, final-score, homework scores). This cycle repeats for the 3rd student “Joe”.
Like test 1, the first end-of-file (F6) button exit the inner while loop (of the read_hw function). The second end-of-file (F6) button exit the outer while loop (of the main program).
The main program then proceeds with the downstream block of code, and output the results accordingly.
Test 3
This time in test 3, I combine a bit of test 1 and test 2 together. i.e. I will use the same set of values, but this time, some of these values shall spread over multiple lines, and some on the same line. I would like to prove that the result should be exactly the same as test 1 and 2, using the hybrid explanations as per test 1 and test 2.
Test 3 – Input and Result
Johnny 70 80 50
60 30
Fred 95 90 100 100 100
Joe
40
40
50
60 50 70 70 50
^Z
^Z
Fred 95
Joe 46
Johnny 66
Process returned 0 (0x0) execution time : 47.050 s
Press any key to continue.
Test 3 – Observation and Explanation
As expect, the result is exactly the same as test 1 and test 2. This has proved that, using the explanation as per test 1 and test 2, as long as the input values are the same, it doesn’t matter whether we spread our data over multiple lines or on the same line. However, I do find the input format of test 2 (i.e. one line per student) is the most tidy and easy-to-understand flat-file format. In fact, most of the flat-files that I deal with at work (such as reading CSV files using SAS) likes this type of format – 1 line per observation (or record). So my recommendation is to stick with the (CSV like) flat-file format used in test 2.
Test 4
In this test, I would like to demonstrate what the result looks like, if I enter no homework for some students.
Test 4 – Input and Result
Johnny 70 80 50 60 30
Leon 100 100
Fred 95 90 100 100 100
Simon 90 90
Joe 40 40 50 60 50 70 70 50
^Z
^Z
Fred 95
Joe 46
Johnny 66
Leon student has done no homework
Simon student has done no homework
Process returned 0 (0x0) execution time : 48.859 s
Press any key to continue.
Test 4 – Observation and Explanation
Note that Leon and Simon have done no homework! And as expected, the program is clever enough to pick this up and store this status for the corresponding Student_info type objects, instead of exiting the program entirely.
This “exception handling” step is carried out during the main.cpp program, between the try and catch exception handling step.
Test 5
This time, I enter 2 lines of input correctly. Then for the 3rd line, I only enter a name (and then hit enter). Then on the 4th line, I enter another name and hit enter. This time the program only processes the first two lines of input and output the results for these two lines. The program ignore the 3rd and 4th invalid lines entirely. This is as expected.
Test 5 – Input and Result
Johnny 70 80 50 60 30
Fred 95 90 100 100 100
Joe
Simon
Fred 95
Johnny 66
Process returned 0 (0x0) execution time : 29.578 s
Press any key to continue.
Test 5 – Observation and Explanation
On the 3rd line, after entering “Joe, the read function (within the Student_info.cpp file) expects a numeric value midterm score. Because the next value “Simon” is not a numeric value, it exit that loop and return an error status (throug the lvalue istream& is). Because of this, the while loop within the main program exits, and proceeds with the downstream process. Also, because the 3rd line never make it to the read_hw function phase, the 3rd Student_info type object was never created. i.e. only the object for student Johnny and Fred were created. Hence the output result only contains these two students.
Conclusion
These tests conclude that the program works as long as the input data is in a consistent and expected format. The flat-file format as per test 2 is probably the best one to use (i.e. one line per record) – as it is easy to understand and consistent. Chapter 4 has really taught me a great deal on partitioning a program, and refreshing me the way std::cin and buffer function. Data extract-transform-load (ETL) is a core process used in industry reading flat-files. This chapter 4 has helped me understanding how C++ handle ETL.
Reference
Koenig, Andrew & Moo, Barbara E., Accelerated C++, Addison-Wesley, 2000