Daily Archives: July 14, 2014

C++, Programming

Accelerated C++ Solution to Exercise 2-10

Exercise 2-10

Explain each of the uses of std:: in the following program:

int main ()
{
    int k = 0;
    while (k != 10)   // invariant: we have written k asterisks so far
    {
        using std::cout;
        cout << "*";
        ++k;
    }
    std::cout << std::endl;   // std:: is required here
    return 0;
}

Solution

Back to basics – what are namespace, names within a namespace, standard library, and iostream header? (refer to page 3 / chapter 0.5 of the book).

  • std:: corresponds to a namespace called std.
  • A namespace (e.g. std) is a collection of related names (e.g. cout, cin, endl). The standard library uses std to contain all the names that it defines.
  • The iostream standard header defines the names (e.g. cout, cin, endl)

i.e. the iostream standard header defines the names cout, cin, endl, and we refer to these names as std::cout, std::cin, std::endl.

Now, let’s explain the uses of std:: in the program.

Within the while loop, we have using std::cout statement to declare that the name cout (residing in namespace std) is made available to the program. i.e. within the while loop scope whenever we have cout, the program “knows” that we are referring to std::cout – the cout of namespace std. The usage of std::cout statement has the life span of only within the while loop scope, as defined by the two curly braces { }. The while loop uses the std::cout to write asterisks on the console window.

Immediately after the while loop scope, we have std::cout – i.e. we need to explicitly specify that we are referring to the cout of the namespace std (and not other namespaces). std::cout is used here to write to the console window.

Lastly, we have the std::endl. Again, we need to explicitly specify that we are referring to the endl of the namespace std (and not other namespaces). std::endl is used for ending the currently line (and start a new line).

Putting this all together, the program does this:

  • Write 10 asterisks to the console output window.
  • End the current line and start a new line.

To run the program however, we must add the iostream header at the top which defines what the like of std::cout, std::endl, etc.

#include <iostream>

Result

**********

Reference

Koenig, Andrew & Moo, Barbara E., Accelerated C++, Addison-Wesley, 2000
C++, Programming

Accelerated C++ Solution to Exercise 2-9

Exercise 2-9

Write a program that asks the user to enter two numbers and tells the user which number is larger than the other.

Solution

Here is my solution strategy:

  • Obtain the two numbers from user. i.e. a and b.
  • Perform a condition check. There are 3 possible cases.
  • Case 1: a == b
  • Case 2: a > b
  • Case 3: a < b
  • Prepare the outcome of each case. e.g. each case can have its own output message.

Putting this together, we have our full program.

#include <iostream>
using std::cout;
using std::cin;
using std::endl;

int main()
{
    cout << "***********************************************************************\n"
         << "*** This program compare 2 numbers and tell you which one is larger ***\n"
         << "***********************************************************************\n";
    cout << endl;
    cout << "Enter the first number (a): ";
    int a;
    cin >> a;
    cout << "Enter the second number (b): ";
    int b;
    cin >> b;
    cout << "a = " << a << ", b = " << b << endl;
    if (a == b)
        {cout << "a == b";}
    else if (a > b)
        {cout << "a > b";}
    else
        {cout << "a < b";}
    return 0;
}

Result

Let’s supply 3 sets of input (representing the 3 cases) and confirm the condition check works.

Case 1: a == b

***********************************************************************
*** This program compare 2 numbers and tell you which one is larger ***
***********************************************************************

Enter the first number (a): 5
Enter the second number (b): 5
a = 5, b = 5
a == b

Case 2: a > b

***********************************************************************
*** This program compare 2 numbers and tell you which one is larger ***
***********************************************************************

Enter the first number (a): 10
Enter the second number (b): 5
a = 10, b = 5
a > b

Case 3: a < b

***********************************************************************
*** This program compare 2 numbers and tell you which one is larger ***
***********************************************************************

Enter the first number (a): 5
Enter the second number (b): 10
a = 5, b = 10
a < b

The condition check for all 3 cases work as expected.

Reference

Koenig, Andrew & Moo, Barbara E., Accelerated C++, Addison-Wesley, 2000
C++, Maths, Programming

Accelerated C++ Solution to Exercise 2-8

2 Comments

Exercise 2-8

Write a program to generate the product of the numbers in the range [1,10).

Solution

The question asks as to compute the product of the numbers within the asymmetric range [1,10). In other words, the product of numbers within the range of 1 to 10, excluding 10. i.e.

1 x 2 x 3 ... x 7 x 8 x 9

Observation: this is the same as 9 factorial (9!). This is the same logic as computing n factorial.

Here outlines my solution strategy at the top level.

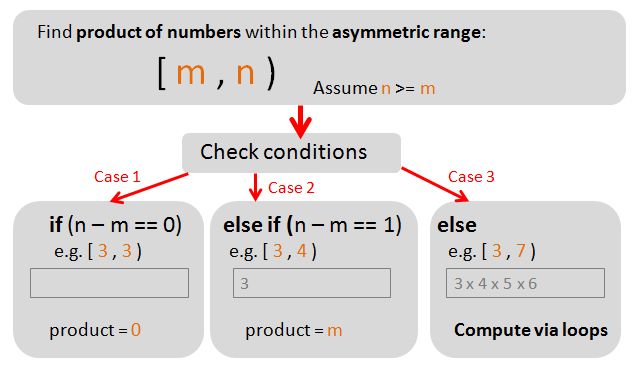
Solution Strategy

Descriptions:

  • Fact: the product of 3 x 4 x 5 (ascending syntax) is the same as 5 x 4 x 3 (descending syntax). So for simplicity, we restrict ourself by only writing in an ascending syntax. i.e. use [3,6), and avoid [5,1) . This is the same as making the assumption of n >= m.
  • Fact: Case 1, if (n-m)=0, e.g. the asymmetric range is [3,3), this is equivalent of saying the range is between 3 and 3 (excluding 3). Because this range is null, the product is also null (zero). No loops required.
  • Fact: Case 2, if (n-m)=1, e.g. the asymmetric range is [3,4), this is equivalent of saying the range is between 3 and 4 (excluding 4). The range is therefore just the number 3 (i.e. m). Likewise, the product is also 3 (i.e. m). No loops required.
  • Fact: Case 3, if (n-m)>=1, e.g. the asymmetric range is [3,7), this is equivalent of saying the range is between 3 and 7 (excluding 7). i.e. we are looking for the product of 3 x 4 x 5 x 6. To compute this we must use loops. The main focus of this post is case 3.

Case 3 Solution Strategy

After spending an entire Sunday afternoon on this question, I eventually spotted a pattern which I believe is consistent and can be leveraged in the forming of our algorithm. To demonstrate this pattern, I have put together some diagrams in PowerPoint and presented as snapshot images below. For clarity, we are going to focus on this particular (arbitrary) asymmetric range as our core example: [3, 7).

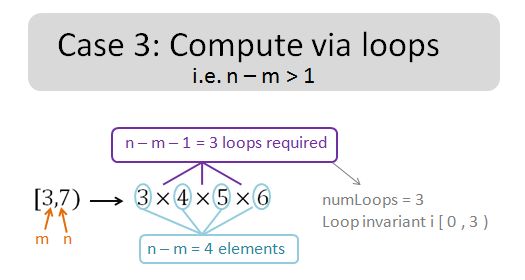
Solution Strategy

 

Observations:

  • The number of elements is always (n-m). there are 4 elements in this case.
  • The number of loops required is always (n-m-1). We need 3 loops in this case. (numLoops = 3).
  • The number of loops required also equals to the number of (multiplication) operator.
  • Knowing the number of loops required enable us to form the loop invariant i [0,numLoops).

Now, let’s try and observe more patterns – what happens at each loop? (See diagram below)

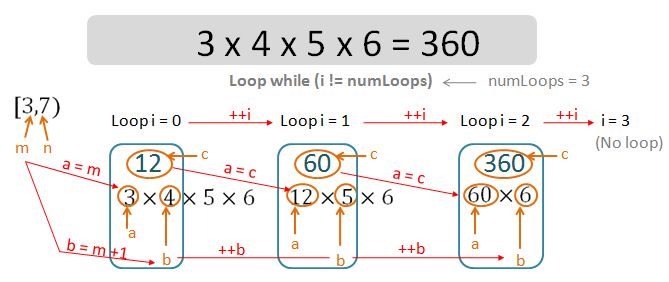
Solution Strategy

Observations:

  • 4 major variables are required.
  • The integer invariant i that controls whether the loop is to go ahead or terminate.
  • The integer variable a – the lower number of the product (a x b).
  • The integer variable b – the higher number of the product (a x b).
  • The integer variable c – the product of (a x b).
  • At the beginning of the very first loop, initialise values of a and b.
  • At the end of each loop, the re-initialise values of a and b.

The final product of [m,n) is the value of c at the end of the very last loop.

For completeness, let’s do a drill down into the loops in greater depth. Bear in mind that for [3,7), the numLoops is n-m-1=3. We need 3 loops. The loop go ahead if the invariant i has not reached numLoops – it starts at 0 (zero), and get increment by 1 at end of each loop.

Invariant i = 0 (Loop)

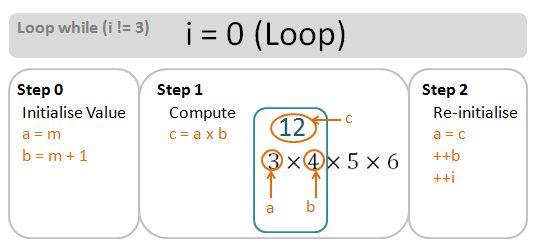
Solution Strategy

Invariant i = 1 (Loop)

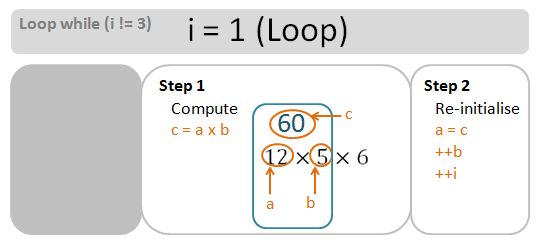
Solution Strategy

Invariant i = 2 (Loop)

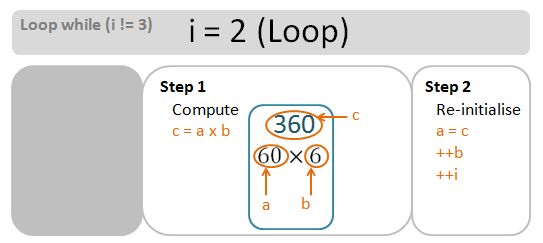
Solution Strategy

Invariant i = 3 (No Loop)

Solution Strategy

At the end of the loop, output the final result. The product of the numbers within the asymmetric range [m,n) is the value of c at the end of the very last loop. The following table summarises this looping process.

Invariant i a b c
0 3 4 12
1 12 5 60
2 60 6 360

Full Program

We should now have all the fundamentals in the making of our program. This is my version of the program. (There are many ways to do this however!)

#include <iostream>
using namespace std;
int main()
{
    cout << "***********************************************************\n"
         << "*** This program computes the product of the numbers    ***\n"
         << "*** in the asymmetric range [m,n).                      ***\n"
         << "*** (Limitation: please ensure m is not larger than n)  ***\n"
         << "*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***\n"
         << "***********************************************************";
    cout << endl;

    // Ask user to supply the startNumber
    cout << "Enter m: ";
    int m;
    cin >> m;

    // Ask user to supply the endNumber
    cout << "Enter n: ";
    int n;
    cin >> n;

    // Algorithm to compute the product of numbers within the asymmetric range [m,n)
    const int startNumber = m ;
    const int endNumber = n;
    const int numElements = endNumber - startNumber;
    const int numLoops = numElements - 1;
    int c;
    if (numElements == 0)
        {c = 0;}
    else if (numElements == 1)
        {c = startNumber;}
    else
    {
        int a = startNumber;
        int b = startNumber + 1;

        cout << " i, a, b, c " << endl;
        for (int i = 0; i != numLoops; ++i)
        {
            c = a * b;
            cout << i << ", " << a << ", " << b << ", " << c << endl;
            a = c;
            ++b;
        }
    }
    cout << "Asymmetric range: [" << startNumber << "," << endNumber << ")" << endl;
    cout << "Number of elements: " << numElements << endl;
    cout << "Number of loops required: " << numLoops << endl;
    cout << "Product of numbers within the asymmetric range = " << c << endl;
    return 0;
}

Result

The program is meant to be robust and be able to deal with any asymmetric range [m,n) as long as (n>=m). Case 1-3 are mainly for prove of concepts. Case 4 is the solution to the question (find product of numbers within the range [1,10).

  • Case 1 – when (n-m)=0. e.g. [3,3)
  • Case 2 – when (n-m)=1. e.g. [3,4)
  • Case 3 – when (n-m)>1. e.g. [3,7)
  • Case 4 – when (n-m)>1. e.g. [1,10)

Case 1 – Asymmetric Range [3,3)

***********************************************************
*** This program computes the product of the numbers    ***
*** in the asymmetric range [m,n).                      ***
*** (Limitation: please ensure m is not larger than n)  ***
*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***
***********************************************************
Enter m: 3
Enter n: 3
Asymmetric range: [3,3)
Number of elements: 0
Number of loops required: 0
Product of numbers within the asymmetric range = 0

Case 2 – Asymmetric Range [3,4)

***********************************************************
*** This program computes the product of the numbers    ***
*** in the asymmetric range [m,n).                      ***
*** (Limitation: please ensure m is not larger than n)  ***
*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***
***********************************************************
Enter m: 3
Enter n: 4
Asymmetric range: [3,4)
Number of elements: 1
Number of loops required: 0
Product of numbers within the asymmetric range = 3

Case 3 – Asymmetric Range [3,7)

***********************************************************
*** This program computes the product of the numbers    ***
*** in the asymmetric range [m,n).                      ***
*** (Limitation: please ensure m is not larger than n)  ***
*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***
***********************************************************
Enter m: 3
Enter n: 7
 i, a, b, c
0, 3, 4, 12
1, 12, 5, 60
2, 60, 6, 360
Asymmetric range: [3,7)
Number of elements: 4
Number of loops required: 3
Product of numbers within the asymmetric range = 360

Case 4- Asymmetric Range [1,10)

***********************************************************
*** This program computes the product of the numbers    ***
*** in the asymmetric range [m,n).                      ***
*** (Limitation: please ensure m is not larger than n)  ***
*** e.g. [3,7) contains elements 3, 4, 5, 6 (but not 7) ***
***********************************************************
Enter m: 1
Enter n: 10
 i, a, b, c
0, 1, 2, 2
1, 2, 3, 6
2, 6, 4, 24
3, 24, 5, 120
4, 120, 6, 720
5, 720, 7, 5040
6, 5040, 8, 40320
7, 40320, 9, 362880
Asymmetric range: [1,10)
Number of elements: 9
Number of loops required: 8
Product of numbers within the asymmetric range = 362880

Compute the N factorial

Note that this program may also be used as a skeleton program for computing factorial. e.g. 5! = 1 x 2 x 3 x 4 x 5. In other words, to compute n! this is effectively the same as computing the internal product of the numbers within the asymmetric range (0, n+1).

Conclusion

The product of the numbers within the asymmetric range [0,10) is 362880, as computed by the program (and verified by calculators). This program might also be used as a skeleton program for computing factorial.

Reference

Koenig, Andrew & Moo, Barbara E., Accelerated C++, Addison-Wesley, 2000